
【题目】在一个试验中,把一种血清注射到500只豚鼠体内,被注射前,这些豚鼠中150只有圆形细胞,250只有椭圆形细胞,100只有不规则形状细胞;被注射后,没有一个具有圆形细胞的豚鼠被感染,50个具有椭圆形细胞的豚鼠被感染,具有不规则形状细胞的豚鼠全部被感染,根据试验结果,估计具有下列类型的细胞的豚鼠被这种血清感染的概率;
(1)圆形细胞;
(2)椭圆形细胞;
(3)不规则形状细胞.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为 (参考数据:![]() ,
,![]() ,
,![]() )
)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,“一带一路”沿线的20国青年评选出了中国“新四大发明”:高铁、支付宝、共享单车和网购.2017年末,“支付宝大行动”用发红包的方法刺激支付宝的使用.某商家统计前5名顾客扫描红包所得金额分别为5.5元,2.1元,3.3元,5.9元,4.7元,商家从这5名顾客中随机抽取3人赠送台历.
(1)求获得台历的三人中至少有一人的红包超过5元的概率;
(2)统计一周内每天使用支付宝付款的人数![]() 与商家每天的净利润
与商家每天的净利润![]() 元,得到7组数据,如表所示,并作出了散点图.
元,得到7组数据,如表所示,并作出了散点图.

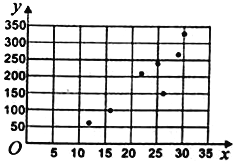
(i)直接根据散点图判断,![]() 与
与![]() 哪一个适合作为每天的净利润的回归方程类型.(
哪一个适合作为每天的净利润的回归方程类型.(![]() 的值取整数)
的值取整数)
(ii)根据(i)的判断,建立![]() 关于
关于![]() 的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
参考数据:
|
|
|
|
22.86 | 194.29 | 268.86 | 3484.29 |
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为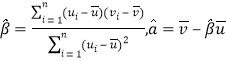 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计ABO血型具有民族和地区差异.在我国H省调查了30488人,四种血型的人数如下:
血型 | A | B | O | AB |
人数/人 | 7704 | 10765 | 8970 | 3049 |
频率 |
(1)计算H省各种血型的频率并填表(精确到0.001);
(2)如果从H省任意调查一个人的血型,那么他是O型血的概率大约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若f(x0)=x0,则称x0为f(x)的“不动点”,若f[f(x0)]=x0,则称x0为f(x)的“稳定点”,函数f(x)的“不动点”和“稳定点”的集合分别记为A和B,即A={x|f(x)=x},B={x|f[f(x)]=x},那么:
(1)函数g(x)=x2-2的“不动点”为______;
(2)集合A与集合B的关系是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接![]() 年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了
年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了![]() 名学生,将他们的比赛成绩(满分为
名学生,将他们的比赛成绩(满分为![]() 分)分为
分)分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
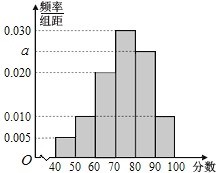
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分”,估计
分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的![]() 名学生中,规定:比赛成绩不低于
名学生中,规定:比赛成绩不低于![]() 分为“优秀”,比赛成绩低于
分为“优秀”,比赛成绩低于![]() 分为“非优秀”.请将下面的
分为“非优秀”.请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() 的中心为坐标原点,焦点
的中心为坐标原点,焦点![]() ,
,![]() 在
在![]() 轴上,且
轴上,且![]() 在抛物线
在抛物线![]() 的准线上,点
的准线上,点![]() 是椭圆
是椭圆![]() 上的一个动点,
上的一个动点,![]() 面积的最大值为
面积的最大值为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过焦点![]() ,
,![]() 作两条平行直线分别交椭圆
作两条平行直线分别交椭圆![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四个点.求四边形
四个点.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com