
【题目】公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为 (参考数据:![]() ,
,![]() ,
,![]() )
)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
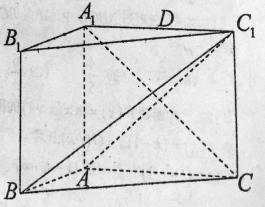
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 是
是![]() 的中点,判断并证明在线段
的中点,判断并证明在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,求点
,若存在,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:  ,其中
,其中![]() 是仪器的月产量.(注:总收益=总成本+利润)
是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数;
的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长,设某地区城乡居民人民币储蓄存款![]() (单位:亿元)的数据如下:
(单位:亿元)的数据如下:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)2018年城乡居民储蓄存款前五名中,有三男和两女.现从这5人中随机选出2人参加某访谈节目,求选中的2人性别不同的概率.
附:回归直线的斜率和截距的最小二乘估计公式分别为:  ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国务院批准从2009年起,将每年8月8日设置为“全民健身日”,为响应国家号召,各地利用已有土地资源建设健身场所.如图,有一个长方形地块![]() ,边
,边![]() 为
为![]() ,
,![]() 为
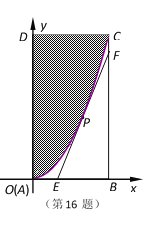
为![]() .地块的一角是草坪(图中阴影部分),其边缘线
.地块的一角是草坪(图中阴影部分),其边缘线![]() 是以直线
是以直线![]() 为对称轴,以
为对称轴,以![]() 为顶点的抛物线的一部分.现要铺设一条过边缘线
为顶点的抛物线的一部分.现要铺设一条过边缘线![]() 上一点
上一点![]() 的直线型隔离带
的直线型隔离带![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(隔离带不能穿越草坪,且占地面积忽略不计),将隔离出的△
上(隔离带不能穿越草坪,且占地面积忽略不计),将隔离出的△![]() 作为健身场所.则△
作为健身场所.则△![]() 的面积为
的面积为![]() 的最大值为____________(单位:
的最大值为____________(单位:![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】针对时下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的女生人数是男生人数的![]() ,男生喜欢抖音的人数占男生人数的
,男生喜欢抖音的人数占男生人数的![]() ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数![]() 若有95%的把握认为是否喜欢抖音和性别有关,则男生至少有( )人.
若有95%的把握认为是否喜欢抖音和性别有关,则男生至少有( )人.
(K2≥k0) | 0.050 | 0.010 |
k0 | 3.841 | 6.635 |
A. 12B. 6C. 10D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水培植物需要一种植物专用营养液,已知每投放![]() (
(![]() 且
且![]() )个单位的营养液,它在水中释放的浓度
)个单位的营养液,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中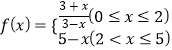 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次2个单位的营养液,则有效时间最多可能达到几天?
(2)若先投放2个单位的营养液,3天后再投放![]() 个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求
个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个试验中,把一种血清注射到500只豚鼠体内,被注射前,这些豚鼠中150只有圆形细胞,250只有椭圆形细胞,100只有不规则形状细胞;被注射后,没有一个具有圆形细胞的豚鼠被感染,50个具有椭圆形细胞的豚鼠被感染,具有不规则形状细胞的豚鼠全部被感染,根据试验结果,估计具有下列类型的细胞的豚鼠被这种血清感染的概率;
(1)圆形细胞;
(2)椭圆形细胞;
(3)不规则形状细胞.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com