
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:  ,其中
,其中![]() 是仪器的月产量.(注:总收益=总成本+利润)
是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数;
的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过椭圆
经过椭圆![]() :
: ![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上的两点,它们在
上的两点,它们在![]() 轴两侧,且
轴两侧,且![]() 的平分线在
的平分线在![]() 轴上,
轴上, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)证明:直线![]() 过定点.
过定点.
【答案】(Ⅰ)![]() .(Ⅱ)直线
.(Ⅱ)直线![]() 过定点
过定点![]() .
.
【解析】【试题分析】(I)根据圆的半径和已知 ![]() ,故
,故![]() ,由此求得椭圆方程.(II)设出直线
,由此求得椭圆方程.(II)设出直线![]() 的方程,联立直线方程与椭圆方程,写出韦达定理,写出
的方程,联立直线方程与椭圆方程,写出韦达定理,写出![]() 的斜率并相加,由此求得直线
的斜率并相加,由此求得直线![]() 过定点
过定点![]() .
.
【试题解析】
(Ⅰ)圆![]() 与
与![]() 轴交点
轴交点![]() 即为椭圆的焦点,圆
即为椭圆的焦点,圆![]() 与
与![]() 轴交点
轴交点![]() 即为椭圆的上下两顶点,所以
即为椭圆的上下两顶点,所以![]() ,
, ![]() .从而
.从而![]() ,
,
因此椭圆![]() 的方程为:
的方程为: ![]() .
.
(Ⅱ)设直线![]() 的方程为
的方程为![]() .
.
由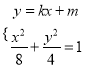 ,消去
,消去![]() 得
得![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
直线![]() 的斜率
的斜率![]()
![]() ;
;
直线![]() 的斜率
的斜率![]()
![]() .
.
![]()
![]()
![]()
![]() .
.
由![]() 的平分线在
的平分线在![]() 轴上,得
轴上,得![]() .又因为
.又因为![]() ,所以
,所以![]() ,
,
所以![]() .
.
因此,直线![]() 过定点
过定点![]() .
.
[点睛]本小题主要考查椭圆方程的求解,考查圆与椭圆的位置关系,考查直线与圆锥曲线位置关系. 涉及直线与椭圆的基本题型有:(1)位置关系的判断.(2)弦长、弦中点问题.(3)轨迹问题.(4)定值、最值及参数范围问题.(5)存在性问题.常用思想方法和技巧有:(1)设而不求.(2)坐标法.(3)根与系数关系.
【题型】解答题
【结束】
21
【题目】已知函数![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)求函数![]() 在
在![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 对任意的
对任意的![]() 都有
都有![]() ,且
,且![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() .
.
①若存在实数![]() ,
,![]() ,使得
,使得![]() 在区间
在区间![]() 上为单调函数,且
上为单调函数,且![]() 取值范围也为
取值范围也为![]() ,求
,求![]() 的取值范围;
的取值范围;
②若函数![]() 的零点都是函数
的零点都是函数![]() 的零点,求
的零点,求![]() 的所有零点.
的所有零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某服装商场,当某一季节即将来临时,季节性服装的价格呈现上升趋势.设一种服装原定价为每件70元,并且每周(7天)每件涨价6元,5周后开始保持每件100元的价格平稳销售;10周后,当季节即将过去时,平均每周每件降价6元,直到16周末,该服装不再销售.
(1)试建立每件的销售价格![]() (单位:元)与周次
(单位:元)与周次![]() 之间的函数解析式;
之间的函数解析式;
(2)若此服装每件每周进价![]() (单位:元)与周次
(单位:元)与周次![]() 之间的关系为
之间的关系为![]() ,
,![]() ,试问该服装第几周的每件销售利润最大?(每件销售利润=每件销售价格-每件进价)
,试问该服装第几周的每件销售利润最大?(每件销售利润=每件销售价格-每件进价)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是
是![]() 的中点,点
的中点,点![]() 沿着路径
沿着路径![]() 在正方形边上运动所经过的路程为
在正方形边上运动所经过的路程为![]() ,
,![]() 的面积为
的面积为![]() .
.

(1)求![]() 的解析式及定义域;
的解析式及定义域;
(2)求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 位置.
位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数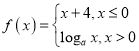 且点
且点![]() 在函数
在函数![]() 的图象上.
的图象上.
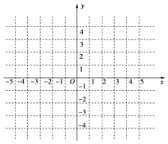
(1)求函数![]() 的解析式,并在图中的直角坐标系中画出函数
的解析式,并在图中的直角坐标系中画出函数![]() 的图象;
的图象;
(2)求不等式![]() 的解集;
的解集;
(3)若方程![]() 有两个不相等的实数根,求实数
有两个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标平面中, ![]() 的两个顶点为
的两个顶点为![]() ,平面内两点
,平面内两点![]() 、
、![]() 同时满足:①
同时满足:①![]() ;②
;②![]() ;③
;③![]() .
.
(1)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,直线
,直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交弦分别为
相交弦分别为![]() ,设弦
,设弦![]() 的中点分别为
的中点分别为![]() .
.
①求四边形![]() 的面积
的面积![]() 的最小值;
的最小值;
②试问:直线![]() 是否恒过一个定点?若过定点,请求出该定点,若不过定点,请说明理由.
是否恒过一个定点?若过定点,请求出该定点,若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com