对于函数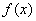
和
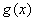，若存在常数
，对于任意
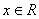，不等式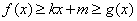
都成立，则称直线
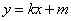是函数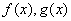
的分界线. 已知函数
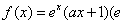为自然对数的底，
为常数）.
(Ⅰ)讨论函数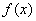的单调性；(Ⅱ)设
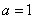，试探究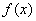函数与函数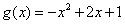
是否存在“分界线”？若存在，求出分界线方程；若不存在，试说明理由.
名校课堂系列答案科目：高中数学 来源： 题型：
已知函数f（x）＝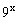
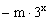+m+1对x∈（0，
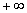）的图象恒在x轴上方，则m的取值范围是 （ ）
A．2－2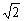
＜m＜2+2 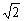B．m＜2C． m＜2+2 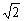D．m≥2+2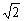
查看答案和解析>>
科目：高中数学 来源： 题型：
将如图所示的三角形数阵中所有的数按从上至下、从左至右的顺序排列成数列a11，a21，a22，a31，a32，…．若所得数列构成一个等差数列，且a11=2，a33=12，则①数阵中的数aii可用i表示为 ；
②若amn+a（m+1）（n+1）=a（m+2）（n+2），则m+n的值为 ．
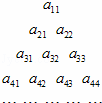
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
， 当
时，
，即
，
在区间
上是增函数，在区间
上是减函数；当
时，
，函数
上的增函数 当
时，
，
恒成立，令
，则
，所以
， 因此：
恒成立，即
恒成立，由
得到：
，
是否恒成立，设
，因为：
，
时，
，
，当
时，
，
，所以
，即
存在“分界线”.
，则P⊙Q= （ ）
B 
C [1，2] D （2，+
）
满足
满足
，则
满足对
，且
，都有
，则
的元素个数为 ． 
（Ⅰ）求函数的定义域，并证明
恒成立，求实数
的取值范围；
时，试比较
与
的大小关系．
,
. 在
中,正数的个数是 （ ）
的前
项和
，则当
时，有( )
（B）
（C）
（D）