
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.
(Ⅰ)求证:DE是⊙O的切线;
(Ⅱ)若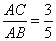 ,求
,求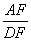 的值.
的值.
(Ⅰ)先证DE⊥OD (Ⅱ)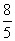
解析试题分析:(1)连结OD,可得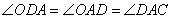
∴OD∥AE 又AE⊥DE ∴DE⊥OD,又OD为半径,∴DE是 的切线
的切线
(2)过D作DH⊥AB于H,则有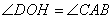
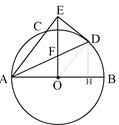
Cos∠DOH=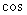 ∠CAB=
∠CAB=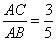
设OD=5x,则AB=10x,OH=3x,DH=4x ∴AH=8x AD2=80x2
由△AED∽△ADB可得 AD2=AE·AB=AE·10x ∴AE=8X
又由△AEF∽△DOF 可得AF∶DF= AE∶OD =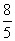 ;∴
;∴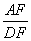 =
=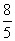
考点:切线的判定与性质;角平分线的定义;平行线的性质;等腰三角形的性质;勾股定理;圆周角定理;相似三角形的判定与性质;锐角三角函数的定义.
点评:本题综合考查了等腰三角形的性质,平行线的性质,切线的性质和判定,相似三角形的性质和判定,锐角三角函数,勾股定理,角平分线定义等知识点的运用,题目较好,综合性强,有一定的难度,主要培养学生综合运用所学知识进行推理的能力.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
(1) 求证:FA∥BE;
(2)求证: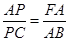 ;
;
(3)若⊙O的直径AB=2,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,
垂是为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点。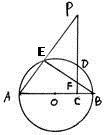
(I)求证:∠PFE=∠PAB;
(II)求证:CD2=CF·CP.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线交CA的延长线于P.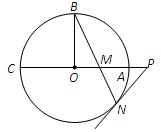
(1)求证:PM2=PA•PC;
(2)若⊙O的半径为2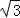 ,OA=
,OA=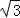 OM,求MN的长.
OM,求MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA, ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.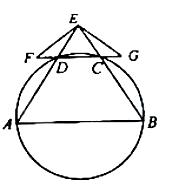
(I)证明:CD//AB;
(II)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com