
如图,四边形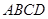 是☉
是☉ 的内接四边形,
的内接四边形, 不经过点
不经过点 ,
, 平分
平分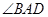 ,经过点
,经过点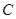 的直线分别交
的直线分别交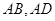 的延长线于点
的延长线于点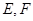 ,且
,且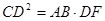 ,证明:
,证明: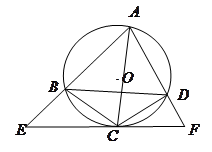
(1)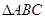 ∽
∽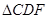 ;
;
(2) 是☉
是☉ 的切线.
的切线.
科目:高中数学 来源: 题型:解答题
(本小题满分10分)选修4—1:几何证明选讲
如图,直线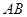 为圆的切线,切点为
为圆的切线,切点为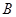 ,点
,点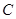 在圆上,
在圆上, 的角平分线
的角平分线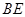 交圆于点
交圆于点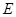 ,
,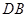 垂直
垂直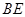 交圆于点
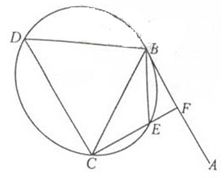
交圆于点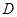 。
。
(Ⅰ)证明: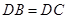 ;
;
(Ⅱ)设圆的半径为 ,
,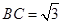 ,延长
,延长 交
交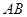 于点
于点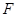 ,求
,求 外接圆的半径。
外接圆的半径。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.
(Ⅰ)求证:DE是⊙O的切线;
(Ⅱ)若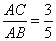 ,求
,求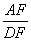 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,直角三角形 的顶点坐标
的顶点坐标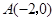 ,直角顶点
,直角顶点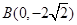 ,顶点
,顶点 在
在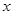 轴上,点
轴上,点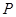 为线段
为线段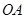 的中点
的中点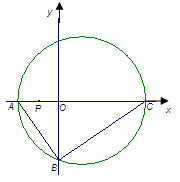
(Ⅰ)求 边所在直线方程;
边所在直线方程;
(Ⅱ) 为直角三角形
为直角三角形 外接圆的圆心,求圆
外接圆的圆心,求圆 的方程;
的方程;
(Ⅲ)若动圆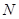 过点
过点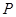 且与圆
且与圆 内切,求动圆
内切,求动圆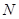 的圆心
的圆心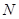 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
(1)①设A1B=x,用x表示AD;②设∠A1AB=θ∈[0º,60º],用θ表示AD
(2)求AD长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)选修41:几何证明选讲
如图,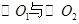 相交于A、B两点,AB是
相交于A、B两点,AB是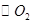 的直径,过A点作
的直径,过A点作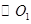 的切线交
的切线交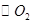 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与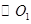 、
、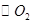 交于C,D两点.
交于C,D两点.
求证:(1)PA·PD=PE·PC; (2)AD=AE.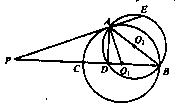
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com