
已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
(1) 求证:FA∥BE;
(2)求证: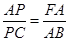 ;
;
(3)若⊙O的直径AB=2,求 的值.
的值.
(1)根据题意,由于∠OAF=∠F ∵∠B=∠F ∴∠OAF=∠B ∴FA∥BE 可知结论。
(2)利用△APC∽△FAC来得到证明。
(3)tan∠F=
解析试题分析:解 证明:(1)在⊙O中,∵直径AB与FP交于点O ∴OA=OF
∴∠OAF=∠F ∵∠B=∠F ∴∠OAF=∠B ∴FA∥BE 3分
(2)∵AC为⊙O的切线,PA是弦 ∴∠PAC=∠F
∵∠C=∠C ∴△APC∽△FAC ∴ 6分
6分
∴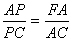 ∵AB="AC" ∴
∵AB="AC" ∴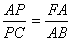 .
.
(3)∵AC切⊙O于点A,CPF为⊙O的割线,则有
AC2=CP•CF=CP(CP+PF),∵PF="AB=AC=2" ∴CP(CP+2)=4
整理得CP2+2CP-4="0," 解得CP=-1±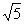
∵CP>0 ∴CP= 8分
8分
∵FP为⊙O的直径 ∴∠FAP=900
由(2)中证得
在Rt△FAP中,tan∠F= 10分
10分
考点:三角形相似以及切割线定理
点评:主要是考查了三角形相似性质的运用,以及切割线定理的运用,属于基础题。


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:解答题
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.,OE交AD于点F.
(I)求证:DE是⊙O的切线;
(II)若 =
= ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.
(Ⅰ)求证:DE是⊙O的切线;
(Ⅱ)若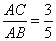 ,求
,求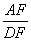 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com