练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知，，，

    (Ⅰ)若，，求的值；

    （Ⅱ）求函数的最小正周期及单调递增区间.


    解:(I) ，，，                     -------2分

        

    (II) ，

       

    所以的最小正周期,                                        

    由得，，

    所以的的单调增区间为.                  


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数（，为常数），当时，函数有极值，若函数有且只有三个零点，则实数的取值范围是            ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点为中心﹐其中﹐分别为原点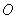到两个顶点的向量﹒若将原点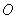到正六角星12个顶点的向量﹐都写成为的形式﹐则的最大值为（    ）

       A. 2             B. 3            C. 4           D. 5 



    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若，则“”是“方程表示双曲线”的（    ）

       A．充分不必要条件　    　　　Ｂ．必要不充分条件　　　　  

     C．充要条件　　　    　       D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知则        _；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列函数在其定义域上既是奇函数又是减函数的（   ）

    A．       B．       C．       D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    交通管理部门为了了解机动车驾驶员（简称驾驶员）对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为，其中甲社区有驾驶员．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为，，，，则这四个社区驾驶员的总人数是（   ）

    A．               B．               C．               D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，圆的半径为，点是弦的中点，，弦过点，且，则的长为      ．

    查看答案和解析>>

    同步练习册答案