
��(��������l 4��)
��ͼ���ڱ߳�Ϊ4������ABCD�У���DAB=60�㣮��E��F�ֱ��ڱ�CD��CB�ϣ���E���C��D���غϣ�EF��AC��EF��AC=O����EF����CEF���۵���PEF��λ�ã�ʹƽ��PEF��ƽ��ABFED��
(��)��֤��BD��ƽ��POA��
(��)��PBȡ����Сֵʱ�������������⣺
(i)������P-BDEF�������
(ii)����Q���� =��
=�� (��
>0)����̽����ֱ��OQ��ƽ��PBD���ɽǵĴ�С�Ƿ�һ������
(��
>0)����̽����ֱ��OQ��ƽ��PBD���ɽǵĴ�С�Ƿ�һ������ ?��˵�����ɣ�
?��˵�����ɣ�

����֤����
�ߡ����� �ĶԽ����ഹֱ��
�ĶԽ����ഹֱ��
��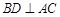 ����
���� ���������������������������������������������� 1��
���������������������������������������������� 1��
��  ����
���� ��
��
�ߡ�ƽ�� ��ƽ��
��ƽ�� ��ƽ��
��ƽ�� ƽ��
ƽ��
 ��
��
�� ƽ��
ƽ�� ��
��
�ࡡ ƽ��
ƽ�� , ���������������������������������������������� 2��
, ���������������������������������������������� 2��
��  ƽ��
ƽ�� ��
��
�ࡡ .�������������������������������������������������������� 3��
.�������������������������������������������������������� 3��
��  ��
��
�ࡡ ƽ��
ƽ�� . �������������������������������������������������� 4��
. �������������������������������������������������� 4��
������ͼ���� Ϊԭ�㣬�����ռ�ֱ������ϵ
Ϊԭ�㣬�����ռ�ֱ������ϵ .���������������������� 5��
.���������������������� 5��
��������
��Ϊ ������
������ Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
�� ��
�� .
.
���� ����
���� ��
�� .
.
����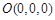 ��
�� ��
�� ��
��
��  ���������������������������������������� 6��
���������������������������������������� 6��
���� ��
��
�� ʱ��
ʱ��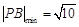 . ��ʱ
. ��ʱ ��
�� ���������������������� 7��
���������������������� 7��
�ɣ���֪�� ƽ��
ƽ��
���� . ������������ 8��
. ������������ 8��
��������� ������Ϊ
������Ϊ ��
��
�ɣ�i��֪�� ����
���� ��
�� ��
�� ��
�� .
.

���� ��
��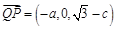 ������������������������������ 9��
������������������������������ 9��
�� ����
����
��

 ��
��
�� ��
��
�� �� �������� 10��
�� �������� 10��
��ƽ�� �ķ�����Ϊ
�ķ�����Ϊ ����
���� ��
��
�� ��
�� ����
���� ����
����
ȡ ����ã�
����ã�
 ��
����
��
���� . �������������������������� 11��
. �������������������������� 11��
��ֱ��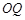 ��ƽ��
��ƽ�� ���ɵĽ�
���ɵĽ� ��
��
��
 ������������������ 12��
������������������ 12��
�֡� ��
�� ������������������������������������������������ 13��
������������������������������������������������ 13��
�� ����
���� ��
��
���ֱ��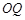 ��ƽ��
��ƽ�� ���ɵĽǴ���
���ɵĽǴ��� �������۳����� ������������������ 14��
�������۳����� ������������������ 14��
����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| x2 |
| 4 |
|
| �� |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ѡ���⣩�������A��B��C��D��С�⣬��ѡ���������⣬���ڴ��ָ���������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮
��ѡ���⣩�������A��B��C��D��С�⣬��ѡ���������⣬���ڴ��ָ���������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 5 |
| �� |
| 4 |
| a |
| b |
| c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������ѧ����2ģ���ҵ�����Ծ� ���ͣ������
19.����С������8�֣���֪������M(��1,1)��ֱ��l��ԲC��x2 + y2��2x + 2y��14 = 0���صõ��ҳ�Ϊ4����ֱ��l�ķ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com