
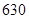 名学生,男女生人数之比为
名学生,男女生人数之比为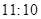 ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为 .
. 列联表:
列联表:| | 否定 | 肯定 | 总计 |
| 男生 | | 10 | |
| 女生 | 30 | | |
| 总计 | | | |
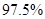 的把握认为态度与性别有关?
的把握认为态度与性别有关? 名男生被抽到,其中
名男生被抽到,其中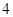 人持否定态度,
人持否定态度, 人持肯定态度;二班有
人持肯定态度;二班有 名女生被抽到,其中
名女生被抽到,其中 人持否定态度,
人持否定态度, 人持肯定态度.
人持肯定态度. 人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.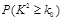 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
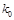 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
| | 否定 | 肯定 | 总计 |
| 男生 | 45 | 10 | 55 |
| 女生 | 30 | 20 | 50 |
| 总计 | 75 | 30 | 105 |
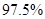 的把握认为态度与性别有关
的把握认为态度与性别有关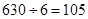 人, 1分
人, 1分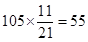 人, 女生
人, 女生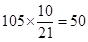 人, 3分
人, 3分| | 否定 | 肯定 | 总计 |
| 男生 | 45 | 10 | 55 |
| 女生 | 30 | 20 | 50 |
| 总计 | 75 | 30 | 105 |
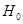 : 学生对体育课改上自习课的态度与性别无关
: 学生对体育课改上自习课的态度与性别无关
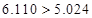 ,
, 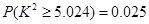
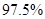 的把握认为态度与性别有关. 8分
的把握认为态度与性别有关. 8分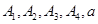 ,
,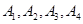 持否定态度,
持否定态度,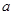 持肯定态度;
持肯定态度;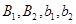 ,
,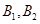 持否定态度,
持否定态度, 持肯定态度.
持肯定态度. ,
,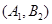 ,
,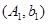 ,
,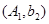 ;
;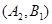 ,
,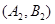 ,
, ,
,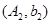 ;
; ,
, ,
, ,
, ;
;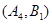 ,
, ,
, ,
,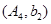 ;
;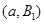 ,
, ,
,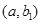 ,
,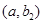 . 10分
. 10分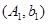 ,
,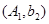 ,
, ,
,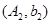 ,
, ,
, ,
, ,
,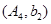 ,
,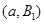 ,
, . 11分
. 11分 人中随机抽取一男一女,其中恰有一人持肯定态度一人持否定态度”事件为
人中随机抽取一男一女,其中恰有一人持肯定态度一人持否定态度”事件为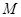 ,则
,则 . 12分
. 12分 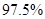 的把握认为态度与性别有关;
的把握认为态度与性别有关;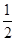 . 13分
. 13分

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
| | 60分 以下 | 61~ 70分 | 71~ 80分 | 81~ 90分 | 91~ 100分 |
| 甲班 (人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班 (人数) | 4 | 8 | 13 | 15 | 10 |
| | 优秀人数 | 非优秀人数 | 总计 |
| 甲班 | | | |
| 乙班 | | | |
| 总计 | | | |
 ,
,
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、第2组
、第2组 、第3组
、第3组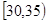 、第4组
、第4组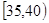 、第5组
、第5组 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示: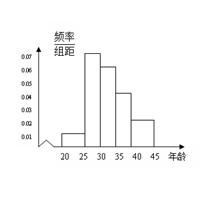
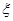 表示抽出的3名志愿者中第3组的人数,求
表示抽出的3名志愿者中第3组的人数,求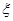 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.500人 | B.1000人 | C.1500人 | D.2000人 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好; 是衡量预报精确度的一个量,它满足
是衡量预报精确度的一个量,它满足 ;
; 和
和 ,它们的随机变量
,它们的随机变量 的观测值
的观测值 来说,
来说, 越小,认为“
越小,认为“ 和
和 有关系”的把握程度越大。
有关系”的把握程度越大。| A.①③ | B.②④ | C.③⑤ | D.②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
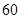 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
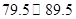 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?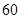 分及以上为及格)
分及以上为及格)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com