
已知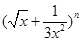 的第五项的二项式系数与第三项的二项式系数的比是
的第五项的二项式系数与第三项的二项式系数的比是 ,
,
(1)求n;
(2)求展开式中常数项.
科目:高中数学 来源: 题型:填空题
现将10个扶贫款的名额分配给某乡镇不同的四个村,要求一个村1个名额,一个村2个名额,一个村3个名额,一个村4个名额,则不同的分配方案种数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
规定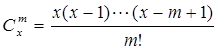 ,其中
,其中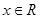 ,
, 是正整数,且
是正整数,且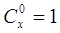 ,这是组合数
,这是组合数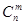 (
( 、
、 是正整数,且
是正整数,且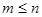 )的一种推广.如当
)的一种推广.如当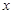 =-5时,
=-5时,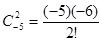
(1)求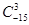 的值;
的值;
(2)设x>0,当x为何值时,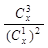 取得最小值?
取得最小值?
(3)组合数的两个性质;
①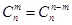 . ②
. ② .
.
是否都能推广到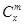 (
(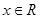 ,
, 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有3名男生,4名女生,在下列不同要求下,求不同的排列方法总数:
(1)选其中5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体排成一排,甲不站在排头也不站在排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻;
(6)全体排成一排,甲、乙两人中间恰好有3人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com