
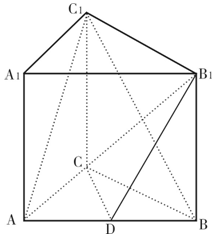
 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.分析 (1)利用勾股定理的逆定理可得AC⊥BC.利用线面垂直的性质定理可得CC1⊥AC,再利用线面垂直的判定定理即可证明结论;
(2)利用直三棱柱的性质、三角形的中位线定理即可得出ED∥AC1,再利用线面平行的判定定理即可证明结论;
解答  证明:(1)∴CC1⊥底面ABC
证明:(1)∴CC1⊥底面ABC
∴CC1⊥AC…(1分)
∴AC=3 BC=4 AB=5
∴AC2+BC2=AB2
∴AC⊥BC…(2分)
∴AC⊥平面BCC1B1…(3分)
∴AC⊥BC1…(4分)
(2)设BC1∩B1C=E,连接DE
∵BCC1B1是矩形,
∴E是BC1的中点…(5分)
又D是AB的中点,在△ABC1中,DE∥AC1…(6分)
又AC1?平面CDB1,DE?平面CDB1
∴AC1∥平面CDB1…(8分)
点评 本题主要考查了勾股定理的逆定理、线面垂直的判定和性质定理、直三棱柱的性质、正方形的性质、三角形的中位线定理、线面平行的判定定理的综合应用,考查了数形结合思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 66 | B. | 76 | C. | 63 | D. | 73 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $4\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{A{C}_{1}}$ | B. | $\overrightarrow{C{A}_{1}}$ | C. | $\overrightarrow{A{D_1}}$ | D. | $\overrightarrow{{D_1}A}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | △ABC中,若a>b,则sinA>sinB | |
| B. | 函数y=f(x)在x=x0处取得极值的充要条件是f'(x0)=0 | |
| C. | 等差数列{an}中,a4=4,a5+a11=16则a12=12 | |
| D. | 双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的焦点到渐近线的距离3. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y-1=0 | B. | x+y-5=0或2x-3y=0 | ||
| C. | x+y-5=0 | D. | x-y-1=0或2x-3y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 天数x(天) | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| 日经济收入Q(万元) | 154 | 180 | 198 | 208 | 210 | 204 | 190 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
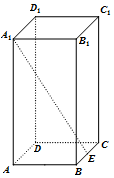 如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )
如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )| A. | 2 | B. | $\frac{{4\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{17}}}{2}$ | D. | $\frac{{2\sqrt{21}}}{21}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com