
| A. | △ABC中,若a>b,则sinA>sinB | |
| B. | 函数y=f(x)在x=x0处取得极值的充要条件是f'(x0)=0 | |
| C. | 等差数列{an}中,a4=4,a5+a11=16则a12=12 | |
| D. | 双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的焦点到渐近线的距离3. |
分析 根据正弦定理,可判断A;根据函数极值点的性质,可判断B;根据等差数列的性质,可判断C;根据双曲线的性质,可判断D.
解答 解:△ABC中,若a>b?2RsinA>2RsinB?sinA>sinB,故A正确;
f'(x0)=0是函数y=f(x)在x=x0处取得极值的必要不充分条件,故B错误;
等差数列{an}中,a4=4,a5+a11=16,则a12=a5+a11-a4=12,故C正确;
双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的焦点到渐近线的距离为b=3,故D正确;
故选:B
点评 本题以命题的真假判断与应用为载体,考查了正弦定理,函数的极值,等差数形的性质,双曲线的性质等知识点,难度中档.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-4 | B. | x=-3 | C. | x=-2 | D. | x=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
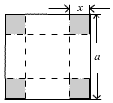 如图所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,当盒子的容积最大时,切去的正方形的边长x为$\frac{a}{6}$.
如图所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,当盒子的容积最大时,切去的正方形的边长x为$\frac{a}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
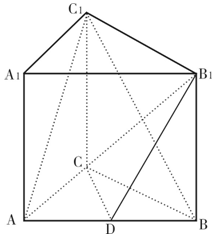 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
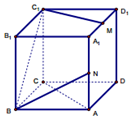 如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 6 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com