
【题目】已知函数![]() ,其中
,其中![]() ,e为自然对数的底数.
,e为自然对数的底数.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若存在![]() (
(![]() ),使得
),使得![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 的递增区间是
的递增区间是![]() ,无递减区间;当
,无递减区间;当![]() 时,
时,![]() 的递增区间是
的递增区间是![]() 和
和![]() ,递减区间是
,递减区间是![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)对![]() 求导,可得
求导,可得![]() 与
与![]() 的值,可得
的值,可得![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)令![]() ,可得
,可得![]() ,对其分
,对其分![]() ,
,![]() 进行讨论,可得
进行讨论,可得![]() 的取值范围及
的取值范围及![]() 的单调区间;
的单调区间;
(3)由(2)知,![]() ,且
,且![]() ,可得
,可得![]() 关于
关于![]() 的函数,对其求导可得其单调性,可得证明.
的函数,对其求导可得其单调性,可得证明.
解:因为![]() 时,
时,![]() 对
对![]() 恒成立,
恒成立,
所以![]() 定义域为
定义域为![]() ,且
,且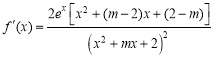 ,
,
(1)当![]() 时,
时,![]() ,
,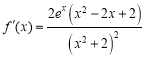 ,所以
,所以![]() ,
,
所以![]() 在
在![]() 处的切线方程为:
处的切线方程为:![]() .
.
(2)令![]() 得,
得,![]() , (※)
, (※)
①当![]() ,即
,即![]() 时,又
时,又![]() ,
,
所以![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() ,解得
,解得![]() 或
或![]() ,又
,又![]() ,所以
,所以![]() 时,
时,
由方程(※)解得,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 的递增区间是
的递增区间是![]() ;
;
当![]() 时,
时,![]() ,
,![]() 的递减区间是
的递减区间是![]() .
.
综上,当![]() 时,
时,![]() 的递增区间是
的递增区间是![]() ,无递减区间;
,无递减区间;
当![]() 时,
时,![]() 的递增区间是
的递增区间是![]() 和
和![]() ,递减区间是
,递减区间是![]() .
.
(3)由(2)知,![]() ,且
,且![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() ,代入上式得
,代入上式得
![]()
![]()
![]()
![]() ,
,
令![]() ,
,![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即证得
,即证得![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,焦点为
,焦点为![]() 的抛物线
的抛物线![]() 的准线被椭圆
的准线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 、
、![]() 到直线
到直线![]() 的距离之积为
的距离之积为![]() ,求证:直线
,求证:直线![]() 与椭圆
与椭圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,
,![]() 为任意实数.
为任意实数.
(1)求证:直线![]() 必与圆
必与圆![]() 相交;
相交;
(2)![]() 为何值时,直线
为何值时,直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 最短?最短弦长是多少?
最短?最短弦长是多少?
(3)若直线![]() 被圆
被圆![]() 截得的弦
截得的弦![]() 的中点为点
的中点为点![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现定义:设![]() 是非零实常数,若对于任意的
是非零实常数,若对于任意的![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“关于的
为“关于的![]() 偶型函数”
偶型函数”
(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的![]() 偶型函数”在区间
偶型函数”在区间![]() 上单调递增,求证在区间
上单调递增,求证在区间![]() 上单调递减
上单调递减
(3)设定义域为![]() 的“关于
的“关于![]() 的偶型函数”
的偶型函数”![]() 是奇函数,若
是奇函数,若![]() ,请猜测
,请猜测![]() 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对函数![]() 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
![]() 函数在
函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
![]() 点
点![]() 是函数图象的一个对称中心;
是函数图象的一个对称中心;
![]() 函数图象关于直线
函数图象关于直线![]() 对称;
对称;
![]() 存在常数
存在常数![]() ,使
,使![]() 对一切实数x均成立,
对一切实数x均成立,
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
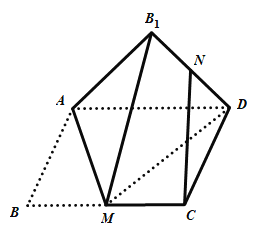
A.存在某个位置,使得![]()
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]()
D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新中国成立70周年以来,党中央国务院高度重视改善人民生活,始终把提高人民生活水平作为一切工作的出发点和落脚点城乡居民收入大幅增长,居民生活发生了翻天覆地的变化.下面是1949年及2015年~2018年中国居民人均可支配收入(元)统计图.以下结论中不正确的是( )
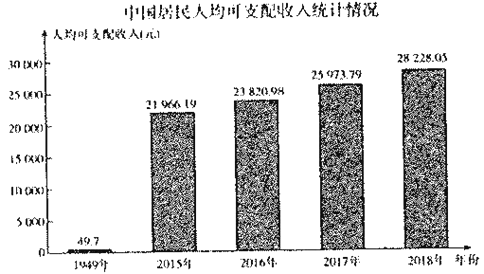
A.20l5年-2018年中国居民人均可支配收入与年份成正相关
B.2018年中居民人均可支配收入超过了1949年的500倍
C.2015年-2018年中国居民人均可支配收入平均超过了24000元
D.2015年-2018年中围居民人均可支配收入都超过了1949年的500倍
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com