
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,焦点为
,焦点为![]() 的抛物线
的抛物线![]() 的准线被椭圆
的准线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 、
、![]() 到直线
到直线![]() 的距离之积为
的距离之积为![]() ,求证:直线
,求证:直线![]() 与椭圆
与椭圆![]() 相切.
相切.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据抛物线的焦点坐标,求得![]() ,根据题意可得知点
,根据题意可得知点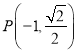 在椭圆
在椭圆![]() 上,利用椭圆的定义可求出
上,利用椭圆的定义可求出![]() 的值,进而得出
的值,进而得出![]() 的值,即可求得椭圆
的值,即可求得椭圆![]() 的标准方程;
的标准方程;
(2)根据(1)中的椭圆方程,求得两个焦点,利用点到直线的距离公式求得![]() 和
和![]() 的关系,再将直线方程代入椭圆方程,计算出
的关系,再将直线方程代入椭圆方程,计算出![]() ,即可证明直线
,即可证明直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)设椭圆![]() 的焦距为
的焦距为![]() ,
,
抛物线![]() 的焦点为
的焦点为![]() ,则
,则![]() ,抛物线
,抛物线![]() 的准线方程为
的准线方程为![]() ,
,
由于抛物线![]() 的准线被椭圆
的准线被椭圆![]() 截得的弦长为
截得的弦长为![]() ,则点
,则点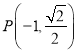 在椭圆
在椭圆![]() 上,
上,
由椭圆的定义得 ,
,![]() ,则
,则![]() ,
,
因此,椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)点![]() 到直线
到直线![]() 的距离
的距离![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
则![]() .
.
①若![]() ,则
,则![]() ,显然不成立;
,显然不成立;
②若![]() ,则
,则![]() .
.
将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立
的方程联立 ,
,
消去![]() 得
得![]() ,
,
则![]() ,
,
因此,直线![]() 与椭圆
与椭圆![]() 相切.
相切.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
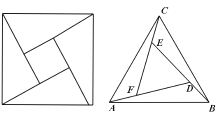
【题目】赵爽是我国古代数学家、天文学家大约在公元222年赵爽为《周碑算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的)类比“赵爽弦图”,赵爽弦图可类似地构造如图所示的图形,它是由个3全等的等边三角形与中间的一个小等边三角形组成的一个大等边三角形,设DF2AF,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为准备参加市运动会,对本校甲、乙两个田径队中![]() 名跳高运动员进行了测试,并用茎叶图表示出本次测试
名跳高运动员进行了测试,并用茎叶图表示出本次测试![]() 人的跳高成绩(单位:
人的跳高成绩(单位:![]() ).跳高成绩在
).跳高成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
)定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
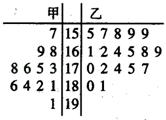
(1)求甲队队员跳高成绩的中位数;
(2)如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取![]() 人,则
人,则![]() 人中“合格”与“不合格”的人数各为多少;
人中“合格”与“不合格”的人数各为多少;
(3)若从所有“合格”运动员中选取![]() 名,用
名,用![]() 表示所选运动员中能参加市运动会开幕式旗林队的人数,试求
表示所选运动员中能参加市运动会开幕式旗林队的人数,试求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家积极推动美丽乡村建设的政策背景下,各地根据当地生态资源打造了众多特色纷呈的乡村旅游胜地.某人意图将自己位于乡村旅游胜地的房子改造成民宿用于出租,在旅游淡季随机选取100天,对当地已有的六间不同价位的民宿进行跟踪,统计其出租率![]() (
(![]() ),设民宿租金为
),设民宿租金为![]() (单位:元/日),得到如图所示的数据散点图.
(单位:元/日),得到如图所示的数据散点图.
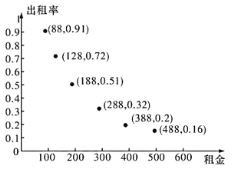
(1)若用“出租率”近似估计旅游淡季民宿每天租出去的概率,求租金为388元的那间民宿在淡季内的三天中至少有2天闲置的概率.
(2)①根据散点图判断,![]() 与
与![]() 哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
②若该地一年中旅游淡季约为280天,在此期间无论民宿是否出租,每天都要付出![]() 的固定成本,若民宿出租,则每天需要再付出
的固定成本,若民宿出租,则每天需要再付出![]() 的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益
的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益![]() 达到最大?
达到最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;![]() .
.
参考数据:记![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面四边形ABCD是菱形,对角线AC与BD交于点O,
中,底面四边形ABCD是菱形,对角线AC与BD交于点O,![]() .
.
![]() 求证:平面
求证:平面![]() 平面PBD;
平面PBD;
![]() 若
若![]() ,
,![]() ,
,![]() ,E为线段PA的中点,求二面角
,E为线段PA的中点,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于受到网络电商的冲击,某品牌的洗衣机在线下的销售受到影响,承受了一定的经济损失,现将![]() 地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
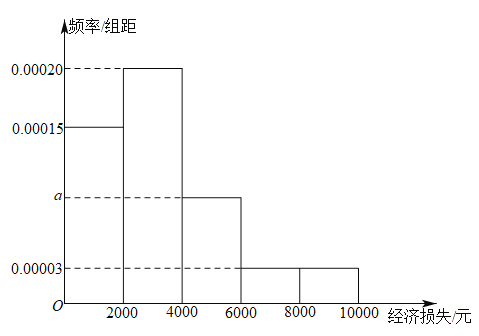
(1)求![]() 的值;
的值;
(2)求![]() 地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
(3)不经过计算,直接给出![]() 地区200家实体店经济损失的平均数
地区200家实体店经济损失的平均数![]() 与6000的大小关系.
与6000的大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com