
判断正误:
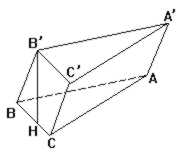
如图, 斜三棱柱ABC-A'B'C'的底面三角形ABC中, ∠C=90°, BC=2, B'在下底面的射影恰为BC中点H, 侧棱与底面夹角为60°, 侧面A'B'BA与侧面B'C'CB的夹角为30°, 则斜三棱柱的侧面积是6+2![]()
( )
体积是2![]()
(
)
|
作CK⊥B'B于K , 连结AK, 由三垂线定理, B'B⊥AK. 所以∠AKC是二面角A-B'B-C平面角, 即∠AKC=30°, 且AKC是三棱柱的直截面. 在△B'BH中, 由∠BHB'=90°, ∠B'BH=60°, BH=1 可得B'B=2
在△BCK中, 由∠BKC=90°, ∠KBC=60°, BC=2可得KC=
在△ACK中, 由∠ACK=90°, ∠AKC=30°, KC=
|
|
1. 过AC作斜三棱柱的直截面KAC, 可先过C点作CK⊥BB'证明平面KAC就是直截面.
2. S侧等于直截面的周长与BB'的乘积
3. V等于直截面的面积与BB1的积.
|


科目:高中数学 来源: 题型:008
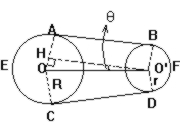
如图, 两轮的半径分别为R, r(R>r), O'H⊥OA, ∠OO'H=θ(弧度), 则连接两轮的皮带传动装置的皮带长为(R+r)π+(R-r)(θ+cotθ)
( )
查看答案和解析>>
科目:高中数学 来源: 题型:008
如图, 已知B、C∈α, AB⊥α于B, CD与α成30°角, ∠BCD = 90°, 若AB = BC = CD =a
则AD的长是![]() a
a
( )
四面体ABCD的体积是![]() a3
a3
( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com