
如图, 已知B、C∈α, AB⊥α于B, CD与α成30°角, ∠BCD = 90°, 若AB = BC = CD =a
则AD的长是![]() a
a
( )
四面体ABCD的体积是![]() a3
a3
( )

|
解: 过D作DH⊥α于H, 则∠DCH=30°,
所以DH= 因为AB⊥α, 所以DH∥AB,过D作DM⊥AB于M,
则DM=BH,且DM∥BH, 所以DH=BM=AM= 又 因为BC=CD=a,∠BCD=90°,
所以BD= 所以面ABHD⊥α, 过C作CO⊥BH于O, 则CO⊥面ABD,
因为∠BCD=90°, ∠BCH=90°, CH= 所以BH=
|
|
①过D作DH⊥α ,DH与BA可确定一个平面. ∠DCH=30° ②过D作DM⊥AB于M, DM∥BH ③在α内作CO⊥BH于O
④VABCD= |


科目:高中数学 来源: 题型:008
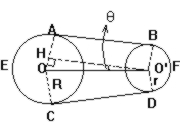
如图, 两轮的半径分别为R, r(R>r), O'H⊥OA, ∠OO'H=θ(弧度), 则连接两轮的皮带传动装置的皮带长为(R+r)π+(R-r)(θ+cotθ)
( )
查看答案和解析>>
科目:高中数学 来源: 题型:008
判断正误:
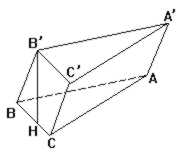
如图, 斜三棱柱ABC-A'B'C'的底面三角形ABC中, ∠C=90°, BC=2, B'在下底面的射影恰为BC中点H, 侧棱与底面夹角为60°, 侧面A'B'BA与侧面B'C'CB的夹角为30°, 则斜三棱柱的侧面积是6+2![]()
( )
体积是2![]()
(
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com