已知二次函数y=f(x)(x∈R)的图象过点(0,-3),且f(x)>0的解集(1,3).
(Ⅰ)求f(x)的解析式;
(Ⅱ)求函数求函数y=f(log2x),x∈[2,16]的最值.
解(Ⅰ)由题意可设二次函数f(x)=a(x-1)(x-3)(a<0)---------------------------
当x=0时,y=-3,即有-3=a(-1)(-3),
解得a=-1,f(x)=-(x-1)(x-3)=-x
2+4x-3,
∴f(x)的解析式为f(x)=-x
2+4x-3.-----------
(Ⅱ)设t=log
2x,∵x∈[2,16],
∴t∈[1,4],
y=f(log
2x)=-
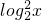
+4log
2x-3=-t
2+4t-3,-----------------------
∴在t∈[1,2]上为增函数,
∴在t∈[2,4]上为减函数,-----------------------------------------------
∴t=2即x=4时,y
最大=1---------------------------------------------
∴t=4即x=16时,y
最小=-3-------------------------------------------
分析:(Ⅰ)设二次函数f(x)=a(x-1)(x-3)(a<0),将(0,-3)代入即可求得f(x)的解析式;
(Ⅱ)设t=log
2x,由x∈[2,16]?t∈[1,2],利用复合函数的单调性即可求得其最大值.
点评:本题考查二次函数的解析式,考查复合函数的单调性与综合应用,考查转化思想与运算能力,属于中档题.

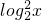 +4log2x-3=-t2+4t-3,-----------------------
+4log2x-3=-t2+4t-3,-----------------------

 已知二次函数y=f(x)的图象如图所示:
已知二次函数y=f(x)的图象如图所示: