
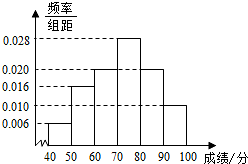
 新津中学高二15班学生参加“六校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.
新津中学高二15班学生参加“六校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.分析 (I)成绩落在[90,100]的有5人,频率为0.010×10,由此能求出该班参加“六校”联考的总人数;
(II)利用频率分布直方图能求出平均分.
(Ⅲ)成绩在[40,50)中共有0.006×10×50=3人,成绩在[90,100)中共有0.010×10×50=5人,要求从成绩在[40,50)和[90,100]的学生共选2人参加某项座谈会,总的基本事件有n=C82=28个,其中2人来自同一分数段的基本事件有m=C32+C52=13个,由此能求出2人来自于同一分数段的概率.
解答 解:(I)该校高三文科(1)班参加“江南十校”联考的总人数为$\frac{5}{0.010×10}$=50(人).
(II)平均分$\overline{x}$=45×0.06+55×0.16+65×0.20+75×0.28+85×0.20+95×0.10=72分.
(Ⅲ) 成绩在[40,50)中共有0.006×10×50=3人,
成绩在[90,100)中共有0.010×10×50=5人,
要求从成绩在[40,50)和[90,100]的学生共选2人参加某项座谈会,
总的基本事件有n=C82=28个,
其中2人来自同一分数段的基本事件有m═C32+C52=13个,
∴2人来自于同一分数段的概率P=$\frac{13}{28}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要注意等可能事件概率计算公式的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
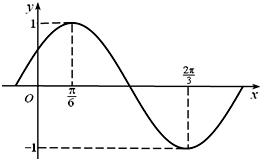 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
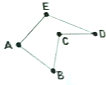 如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )
如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )| A. | $\frac{10}{81}$ | B. | $\frac{1}{9}$ | C. | $\frac{8}{81}$ | D. | $\frac{7}{81}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{kn}{m}$ | B. | $\frac{km}{n}$ | C. | k+m-n | D. | k+m+n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com