
分析 (1)由Sn=$\frac{3}{2}$n2+$\frac{1}{2}$n,利用当n≥2时,an=Sn-Sn-1,又当n=1时,a1=S1,可得an.由b1+b4=18,b2•b3=b1b4=32.可得b1,b4是一元二次方程x2-18x+32=0的两根,解出即可得出.
(2)cn=an•bn=(3n-1)•2n.利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)∵Sn=$\frac{3}{2}$n2+$\frac{1}{2}$n,
∴当n≥2时,an=Sn-Sn-1=$\frac{3}{2}$n2+$\frac{1}{2}$n-$[\frac{3}{2}(n-1)^{2}+\frac{1}{2}(n-1)]$=3n-1,
又当n=1时,a1=S1=2,也符合上式.
∴an=3n-1.
∵b1+b4=18,b2•b3=b1b4=32.
∴b1,b4是一元二次方程x2-18x+32=0的两根,
解得x=2,16.
又b4>b1,
∴b4=16,b1=2,
∴2q3=16,
解得q=2.
∴bn=2n.
(2)cn=an•bn=(3n-1)•2n.
∴数列{Cn}的前n项和Tn=2×2+5×22+8×23+…+(3n-1)×2n,
2Tn=2×22+5×23+…+(3n-4)×2n+(3n-1)×2n+1,
∴-Tn=22+3×22+3×23+…+3×2n-(3n-1)×2n+1=$3×\frac{2({2}^{n}-1)}{2-1}$-2-(3n-1)×2n+1=(4-3n)×2n+1-8,
∴Tn=(3n-4)×2n+1+8.
点评 本题考查了递推式的应用、“错位相减法”等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
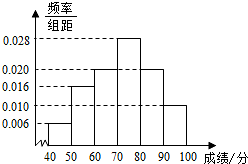 新津中学高二15班学生参加“六校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.
新津中学高二15班学生参加“六校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行于同一平面的两个平面平行 | |
| B. | 平行于同一直线的两个平面平行 | |
| C. | 如果一条直线与两个平行平面中的一个相交,则也与另一个平面相交 | |
| D. | 一条直线与两个平行平面所成的角相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com