
分析 (1)根据不等式的解集有一个元素,写出判别式要满足的条件,求出a的值,把所求的两个数值代入解析式进行检验,看哪一个符合单调性,求出a的值;
(2)根据数列{an}的前n项和Sn=f(n),写出前n项和的表示式,根据由前n项和求通项的方法写出数列的通项,验证首项是否符合所求的通项,得到是一个分段形式;
(3)构造出两个新数列,要求数列{Cn}的前n项和,把数列分成三部分来求,整理出最简形式,根据Tn-n>m对(n∈N*,n≥2)恒成立可转化为:m<16+$\frac{1}{27}$+n-$\frac{1}{{3}^{n+1}}$,对n∈N*,n≥2恒成立,根据16+$\frac{1}{27}$+n-$\frac{1}{{3}^{n+1}}$是关于n的增函数,得到结论.
解答 解:(1)∵f(x)≤0的解集有且只有一个元素,
∴△=a2-4a=0⇒a=0或a=4,
当a=4时,函数f(x)=x2-4x+4在(0,2)上递减,
故存在0<x1<x2,使得不等式f(x1)>f(x2)成立,
当a=0时,函数f(x)=x2在(0,+∞)上递增,
故不存在0<x1<x2,使得不等式f(x1)>f(x2)成立,
综上,得a=4,f(x)=x2-4x+4;
(2)由(1)可知Sn=n2-4n+4,当n=1时,a1=s1=1,
当n≥2时,an=sn-sn-1=(n2-4n+4)-[(n-1)2-4(n-1)+4]=2n-5.
∴an=$\left\{\begin{array}{l}{1,n=1}\\{2n-5,n≥2}\end{array}\right.$.
(3)∵bn=($\sqrt{3}$)${\;}^{{a}_{n}+5}$=$\left\{\begin{array}{l}{27,n=1}\\{{3}^{n},n≥2}\end{array}\right.$,
∴b1=27,c1=18-$\frac{2}{27}$,
n≥2时,cn=2+$\frac{1}{{3}^{n}}$-$\frac{1}{{3}^{n+1}}$,
Tn=c1+c2+…+cn=18-$\frac{2}{27}$+2(n-1)+($\frac{1}{9}$-$\frac{1}{27}$+$\frac{1}{27}$-$\frac{1}{81}$+…+$\frac{1}{{3}^{n}}$-$\frac{1}{{3}^{n+1}}$)
=18-$\frac{2}{27}$+2(n-1)+$\frac{1}{9}$-$\frac{1}{{3}^{n+1}}$=16+$\frac{1}{27}$+2n-$\frac{1}{{3}^{n+1}}$,
Tn-n>m对(n∈N*,n≥2)恒成立
可转化为:m<16+$\frac{1}{27}$+n-$\frac{1}{{3}^{n+1}}$,对n∈N*,n≥2恒成立,
因为16+$\frac{1}{27}$+n-$\frac{1}{{3}^{n+1}}$是关于n的增函数,
所以当n=2时,其取得最小值18,
所以m<18.
点评 本题考查数列与函数的综合,本题解题的关键是根据所给的条件构造新数列,求新数列的和,这里利用数列的求和的基本方法即分组,注意本题中对于特殊项的验证.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
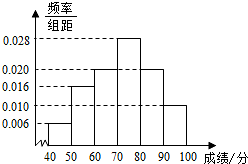 新津中学高二15班学生参加“六校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.
新津中学高二15班学生参加“六校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com