
分析 ?x0∈R,不等式log2(4-a)≥|x0-3|+|x0-1|成立,只需求出f(x)=|x-3|+|x-1|的最小值即可.
解答 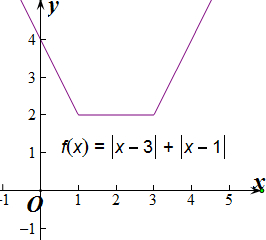 解:设f(x)=|x-3|+|x-1|,
解:设f(x)=|x-3|+|x-1|,
若当x≥3时,f(x)=x-3+x-1=2x-4∈[2,+∞),
当1<x<3时,f(x)=3-x+x-1=2,
当x≤1时,f(x)=-x+3-x+1=-2x+4∈[2,+∞),
图象如图所示:
∴函数f(x)的最小值为2,
要使不等式log2(4-a)≥|x0-3|+|x0-1|成立,
log2(4-a)≥2成立,
即0<4-a≤4,
即0≤a<4,
故实数a的取值范围是[0,4),
故答案为:[0,4)
点评 本题主要考查不等式成立问题,将不等式成立转化为求函数的最值是解决本题的关键,考查绝对值函数的性质.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
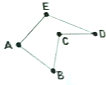 如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )
如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )| A. | $\frac{10}{81}$ | B. | $\frac{1}{9}$ | C. | $\frac{8}{81}$ | D. | $\frac{7}{81}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{3}$,0) | B. | ($\frac{π}{6}$,0) | C. | (-$\frac{π}{3}$,0) | D. | (-$\frac{π}{6}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{kn}{m}$ | B. | $\frac{km}{n}$ | C. | k+m-n | D. | k+m+n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值,无最小值 | B. | 有最大值和最小值 | ||
| C. | 有最小值,无最大值 | D. | 无最值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com