
分析 不妨令a1=$\frac{1}{3}$,a2=$\frac{2}{3}$,b1=$\frac{1}{3}$,b2=$\frac{2}{3}$,分别求出A,B,比较即可
解答 解:∵a2>a1>0,b2>b1>0,且a1+a2=b1+b2=1,
不妨令a1=$\frac{1}{3}$,a2=$\frac{2}{3}$,b1=$\frac{1}{3}$,b2=$\frac{2}{3}$,
A=a1b1+a2b2=$\frac{1}{9}$+$\frac{4}{9}$=$\frac{5}{9}$,B=a1b2+a2b1=$\frac{2}{9}$+$\frac{2}{9}$=$\frac{4}{9}$,
∵C=$\frac{1}{2}$=$\frac{4.5}{9}$
∴B<C<A
故答案为:B<C<A.
点评 本题主要考查不等式与不等关系,利用特殊值代入法比较几个式子在限定条件下的大小关系,是一种简单有效的方法,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | x→y=|x| | B. | x→y=$\frac{1}{{{{({x-1})}^2}}}$ | C. | $x→y={({\frac{1}{2}})^x}$ | D. | $x→y=\sqrt{{{({\frac{1}{2}})}^x}-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,-1] | C. | (3,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
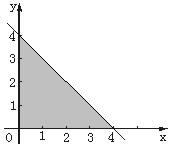 将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所出现的点数﹒图中三角形阴影部分的三个顶点为(0,0)、(4,0)和(0,4).
将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所出现的点数﹒图中三角形阴影部分的三个顶点为(0,0)、(4,0)和(0,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com