
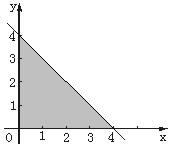
 将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所出现的点数﹒图中三角形阴影部分的三个顶点为(0,0)、(4,0)和(0,4).
将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所出现的点数﹒图中三角形阴影部分的三个顶点为(0,0)、(4,0)和(0,4).分析 (1)由题意知,本题是一个古典概型,试验发生包含的基本事件总数为6×6,画出图形,满足条件的事件A可以列举出有6个整点,根据古典概型概率公式得到结果.
(2)点P(a,b)落在x+y=m(m为常数)的直线上,且使此事件的概率最大,只需基本事件最多,由x,y∈[1,6],画出图形,直线x+y=m过(1,6)时适合,求得x+y=7,此时有6个整点,得到结果.
解答 解:(1)基本事件总数为6×6=36﹒…(2分)
当a=1时,b=1,2,3;
当a=2时,b=1,2;
当a=3时,b=1﹒
共有(1,1),(1,2),(1,3),(2,1),
(2,2),(3,1)6个点落在条件区域内,
∴P(A)═$\frac{1}{6}$﹒…(6分)
(2)当m=7时,…(9分)
(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)共有6种,
此时P=$\frac{6}{36}$=$\frac{1}{6}$最大﹒…(12分)
点评 本题考查古典概型,在解题时要利用图形判断出满足条件的事件数,本题利用数形结合的知识,是一个综合题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (-2,+∞) | C. | (-2,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或3 | B. | 1 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 简单随机抽样法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 抽签法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
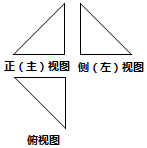 已知某几何体的正(主)视图,侧(左)视图和俯视图均为斜边长为$\sqrt{2}$的等腰直角三角形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为( )
已知某几何体的正(主)视图,侧(左)视图和俯视图均为斜边长为$\sqrt{2}$的等腰直角三角形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为( )| A. | 4π | B. | 3π | C. | 2π | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 3 | C. | 6 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com