
分析 根据圆的标准方程结合$\sqrt{{x^2}+{y^2}}$的几何意义利用数形结合即可得到结论.
解答 解:x2+y2-4x+6y+4=0等价为(x-2)2+(y+3)2=3,则圆心C(2,-3),半径R=3.
$\sqrt{{x^2}+{y^2}}$的几何意义为圆上的点到原点距离.
原点到圆心的距离d=$\sqrt{13}$,
则圆上点到圆的最小值为|R-d|=$\sqrt{13}$-3,
则$\sqrt{{x^2}+{y^2}}$的最小值为$\sqrt{13}$-3.
故答案为$\sqrt{13}$-3
点评 本题主要考查圆的方程的应用,把圆的一般方程化为圆的标准方程并会由圆的标准方程找出圆心坐标与半径是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
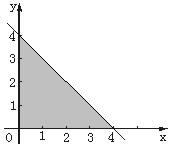 将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所出现的点数﹒图中三角形阴影部分的三个顶点为(0,0)、(4,0)和(0,4).
将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所出现的点数﹒图中三角形阴影部分的三个顶点为(0,0)、(4,0)和(0,4).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知二次函数y=-x2+2x+3
已知二次函数y=-x2+2x+3查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com