
分析 (1)若函数f(x)在区间[-1,1]上不单调,则函数图象的对称轴x=$-\frac{a}{2}$∈[-1,1],解得答案;
(2)由|a|≥2得:a≥2,或a≤-2,则M(a,b)=|f(x)|max=max{|f(-1)|,|f(1)|}=$\left\{\begin{array}{l}|1+a+b|.a+ab≥0\\|1-a+b|.a+ab<0\end{array}\right.$,进而可证得M(a,b)≥2.
解答 解:(1)由题意知:
函数f(x)的对称轴为x=$-\frac{a}{2}$----------------------(2分)
∵函数f(x)在区间[-1,1]上不单调,
∴$-\frac{a}{2}$∈[-1,1]----------------------------------------------(6分)
∴a∈[-2,2]--------------------------------------------(8分)
证明:(2)由|a|≥2得:a≥2,或a≤-2,-------------------(9分)
而函数f(x)的对称轴为直线x=$-\frac{a}{2}$,
M(a,b)=|f(x)|max=max{|f(-1)|,|f(1)|}=$\left\{\begin{array}{l}|1+a+b|.a+ab≥0\\|1-a+b|.a+ab<0\end{array}\right.$---------------------------(13分)
则4≤2|a|≤|1+a+b|+|1-a+b|≤2M(a,b)---------------(14分)
即M(a,b)≥2----------------------------------------------(15分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,-1] | C. | (3,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
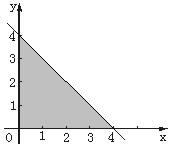 将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所出现的点数﹒图中三角形阴影部分的三个顶点为(0,0)、(4,0)和(0,4).
将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所出现的点数﹒图中三角形阴影部分的三个顶点为(0,0)、(4,0)和(0,4).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com