
(1)讨论函数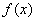 的单调性;
的单调性;
(2)对于任意正实数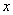 ,不等式
,不等式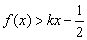 恒成立,求实数
恒成立,求实数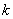 的取值范围;
的取值范围;
(3)是否存在最小的正常数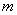 ,使得:当
,使得:当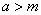 时,对于任意正实数
时,对于任意正实数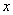 ,不等式
,不等式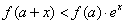 恒成立?给出你的结论,并说明结论的合理性.
恒成立?给出你的结论,并说明结论的合理性.
⑵由于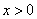 ,所以
,所以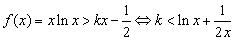 .构造函数
.构造函数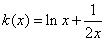 ,则令
,则令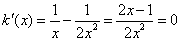 ,得
,得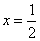 .当
.当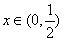 时,
时,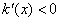 ;当
;当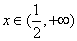 时,
时,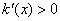 .所以函数在点
.所以函数在点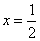 处取得最小值,即
处取得最小值,即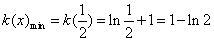 .
.
因此所求的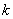 的取值范围是
的取值范围是 . (7分)
. (7分)
⑶结论:这样的最小正常数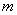 存在. 解释如下:
存在. 解释如下:
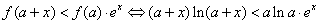
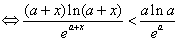 .
.
构造函数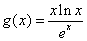 ,则问题就是要求
,则问题就是要求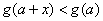 恒成立. (9分)
恒成立. (9分)
对于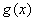 求导得
求导得  .
.
令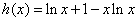 ,则
,则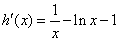 ,显然
,显然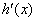 是减函数.
是减函数.
又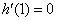 ,所以函数
,所以函数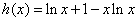 在
在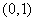 上是增函数,在
上是增函数,在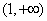 上是减函数,而
上是减函数,而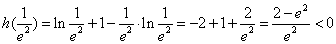 ,
,
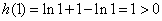 ,
,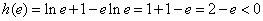 .
.
所以函数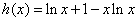 在区间
在区间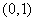 和
和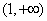 上各有一个零点,令为
上各有一个零点,令为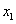 和
和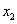
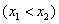 ,并且有: 在区间
,并且有: 在区间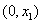 和
和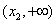 上,
上,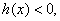 即
即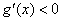 ;在区间
;在区间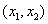 上,
上,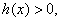 即
即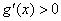 . 从而可知函数
. 从而可知函数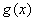 在区间
在区间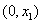 和
和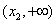 上单调递减,在区间
上单调递减,在区间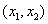 上单调递增.
上单调递增. 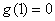 ,当
,当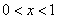 时,
时,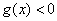 ;当
;当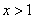 时,
时,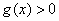 . 还有
. 还有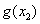 是函数的极大值,也是最大值.
是函数的极大值,也是最大值.
题目要找的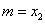 ,理由是:
,理由是:
当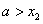 时,对于任意非零正数
时,对于任意非零正数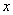 ,
,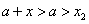 ,而
,而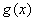 在
在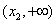 上单调递减,所以
上单调递减,所以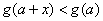 一定恒成立,即题目所要求的不等式恒成立,说明
一定恒成立,即题目所要求的不等式恒成立,说明 ;
;
当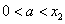 时,取
时,取 ,显然
,显然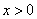 且
且 ,题目所要求的不等式不恒成立,说明
,题目所要求的不等式不恒成立,说明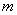 不能比
不能比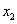 小.
小.
综合可知,题目所要寻求的最小正常数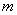 就是
就是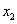 ,即存在最小正常数
,即存在最小正常数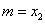 ,当
,当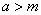 时,对于任意正实数
时,对于任意正实数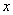 ,不等式
,不等式 恒成立. (12分)
恒成立. (12分)
( 注意:对于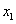 和
和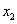 的存在性也可以如下处理:
的存在性也可以如下处理:
令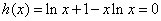 ,即
,即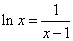 . 作出基本函数
. 作出基本函数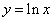 和
和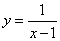 的图像,借助于它们的图像有两个交点很容易知道方程
的图像,借助于它们的图像有两个交点很容易知道方程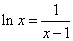 有两个正实数根
有两个正实数根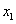 和
和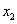 ,且
,且 ,
,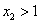 (实际上
(实际上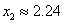 ),可知函数
),可知函数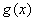 在区间
在区间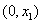 和
和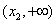 上单调递减,在区间
上单调递减,在区间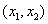 上单调递增.
上单调递增.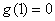 ,当
,当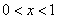 时,
时,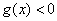 ;当
;当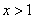 时,
时,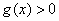 . 还有
. 还有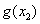 是函数的极大值,也是最大值. )
是函数的极大值,也是最大值. )


科目:高中数学 来源: 题型:
某工厂36名工人的年龄数据如下表:
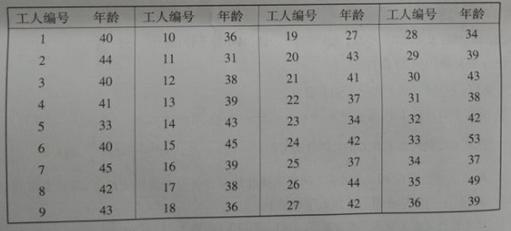
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值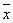 的方差s2;
的方差s2;
(3)36名工人中年龄在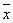 -s与
-s与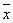 +s之间有多少人?所占的百分比是多少?(精确到0.01%)
+s之间有多少人?所占的百分比是多少?(精确到0.01%)
查看答案和解析>>
科目:高中数学 来源: 题型:
在极坐标系中,曲线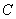 的极坐标方程为
的极坐标方程为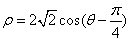 ,以极点
,以极点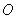 为原点,极轴为
为原点,极轴为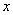 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线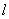 的参数方程为
的参数方程为 (
(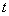 为参数),试判断直线
为参数),试判断直线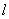 与曲线
与曲线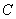 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com