
【题目】点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点, ![]() 两点关于
两点关于![]() 轴对称,过点
轴对称,过点![]() 任作直线交抛物线
任作直线交抛物线![]() 于
于![]() 两点.(Ⅰ)求证:
两点.(Ⅰ)求证: ![]() ;
;
(Ⅱ)若点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,试求所有满足条件的直线
,试求所有满足条件的直线![]() 的解析式.
的解析式.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)利用抛物线![]() 的图象上点的坐标特征,待定系数法球函数解析式,根与系数的关系和相似三角形的判定与性质解答即可;
的图象上点的坐标特征,待定系数法球函数解析式,根与系数的关系和相似三角形的判定与性质解答即可;
(2)利用(1)中已知与结论,继续由相似三角形,根与系数的关系、函数解析式求得结果.
试题解析:
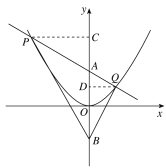
解:(1)如图,分别过点![]() 作为
作为![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .设点
.设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .设直线
.设直线![]() 的函数解析式为
的函数解析式为![]() ,并设
,并设![]() 的坐标分别为
的坐标分别为![]() .由
.由 得
得![]() ,于是
,于是![]() ,即
,即![]() .
.
于是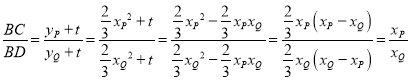 .
.
又因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ∽
∽![]() ,故
,故![]() .
.
(2)设![]() ,不妨设
,不妨设![]() ,由(1)可知
,由(1)可知![]()
![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ∽
∽![]() .于是
.于是![]() ,即
,即![]() ,
,
所以![]() ,由(1)中
,由(1)中![]() ,即
,即![]() ,所以
,所以![]() ,
,
于是可求得![]() .将
.将![]() 代入
代入![]() ,得到点
,得到点![]() 的坐标(
的坐标(![]() ).
).
再将点![]() 的坐标代入
的坐标代入![]() ,求得
,求得![]() .所以
.所以![]() 解析式为
解析式为![]() .
.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1,a14=b4.
(1)求{an}的通项公式;
(2)设cn=an+bn,求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间![]() 上的函数
上的函数![]() ,其中常数
,其中常数![]() .
.
(1)若函数![]() 分别在区间
分别在区间![]() 上单调,试求
上单调,试求![]() 的取值范围;
的取值范围;
(2)当![]() 时,方程
时,方程![]() 有四个不相等的实根
有四个不相等的实根![]() .
.
①证明: ![]() ;
;
②是否存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 单调,且
单调,且![]() 的取值范围为
的取值范围为![]() ,若存在,求出
,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新一届班委会的7名成员有![]() 、
、![]() 、
、![]() 三人是上一届的成员,现对7名成员进行如下分工.
三人是上一届的成员,现对7名成员进行如下分工.
(Ⅰ)若正、副班长两职只能由![]() 、
、![]() 、
、![]() 三人选两人担任,则有多少种分工方案?
三人选两人担任,则有多少种分工方案?
(Ⅱ)若![]() 、
、![]() 、
、![]() 三人不能再担任上一届各自的职务,则有多少种分工方案?
三人不能再担任上一届各自的职务,则有多少种分工方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据以往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为
(升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为
(米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() (万元)与销售额
(万元)与销售额![]() (万元)之间有如下的对应数据:
(万元)之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求回归直线方程;
(2)据此估计广告费用为12万元时的销售额约为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com