练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设a=
    ∫
    π
    2
    0
    (sinx+cosx)dx    ，则二项式(ax-
    1
    x
    )6    展开式中常数项是（　　）
    A．160B．-160C．180D．-180
    由于 a=
    ∫
    π
    2
    0
    (sinx+cosx)dx    =（sinx-cosx）
    |
    π
    2
    0
    =2，则二项式(ax-
    1
    x
    )6    即 (2x-
    1
    x
    )    6    ，
    它的展开式的通项公式为 Tr+1=
    Cr6
    •（-1）r•（2x）6-r•x-r=(-1)r• 
    C r6
    • 2 6-r    •x6-2r．
    令x的幂指数6-2r=0，解得 r=3，
    故二项式(ax-
    1
    x
    )6    展开式中常数项是 (-1)3• 
    C 36
    • 2 6-3    =-160，
    故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    选做题：在A、B、C、D四小题中只能选做2题，每小题10分，共20分．解答应写出文字说明、证明过程或演算步骤．
    A．选修4-1：几何证明选讲
    如图，PA切⊙O于点A，D为PA的中点，过点D引割线交⊙O于B、C两点．求证：∠DPB=∠DCP．
    B．选修4-2：矩阵与变换
    设M=
    .
    10
    02
    .
    ，N=
    .
    1
    2
    		0
    01
    .
    ，试求曲线y=sinx在矩阵MN变换下的曲线方程．
    C．选修4-4：坐标系与参数方程
    在极坐标系中，圆C的极坐标方程为ρ=
    		2
    cos(θ+
    π
    4
    )    ，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
    x=1+
    4
    5
    t
    y=-1-
    3
    5
    t
    （t为参数），求直线l被圆C所截得的弦长．
    D．选修4-5：不等式选讲
    解不等式：|2x+1|-|x-4|＜2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

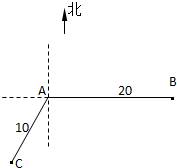    如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救、甲船立即前往救援，同时把消息告知在甲船的南偏西30°，相距10海里C处的乙船．
    （Ⅰ）求处于C处的乙船和遇险渔船间的距离；
    （Ⅱ）设乙船沿直线CB方向前往B处救援，其方向与
    CA
    成θ角，求f(x)=sin2θsinx+
    		3
    4
    cos2θcosx    （x∈R）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•河东区二模）设a=
    ∫
    π
    2
    0
    (sinx+cosx)dx    ，则二项式(ax-
    1
    x
    )6    展开式中常数项是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量a=(cosx,-sinx),b=(sinx,-cosx),设函数f(x)=a·b-1.

    (1)求f(x)的最大值M、最小正周期和单调递增区间；

    (2)20个互不相等的正数xn满足f(xn)=M,且xn＜20π(n∈N*),求x1+x2+…+x20的值.

    查看答案和解析>>

    同步练习册答案