已知|z1|=3,|z1+z2|=5,|z1-z2|=7,则|z2|=________.

分析:根据所给的两个复数的和与差的模长和一个复数的模长,|z
1|,|z
1+z
2|,|z
1-z
2|,|z
2|四个线段组成以|z
1|,|z
2|为邻边,|z
1+z
2|,|z
1-z
2|为对角线的平行四边形,利用三角形中余弦定理求出结果.
解答:∵|z
1|,|z
1+z
2|,|z
1-z
2|,|z
2|四个线段组成以|z
1|,|z
2|为邻边,
|z
1+z
2|,|z
1-z
2|为对角线的平行四边形,
在|z
1|,|z
1+z
2|,|z
1-z
2|组成的三角形中,
|z
1|对应的角的余弦值是
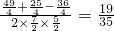
∴|z
2|
2=
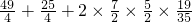
=28,
∴|z
2|=2

,
故答案为:2

点评:本题考查复数求模长,但是,本题所应用的是平行四边形的性质和余弦定理,本题是一个数形结合的问题,注意解题过程中的数字运算.


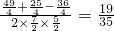
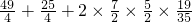 =28,
=28, ,
,


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案