
分析 写出原命题的否定,可判断①;判断两个平面的位置关系,可判断②;根据充要条件的定义,可判断③;求出PA+PB+PC的值,可判断④.
解答 解:若p:?x0∈R,x${\;}_{0}^{2}$-x0>0,则¬p:?x∈R,x2-x≤0,故①错误;
若m⊥α,m∥n,则n⊥α,又由n∥β,则α⊥β,故②正确;
y=kx+2k恒过(-2,0)点,
若“?k∈R,y=kx+2k与x2+y2+mx=0都有公共点”
则(-2,0)在圆x2+y2+mx=0内部,
即4-2m<0,解得:m>2,
故“m>2”是“?k∈R,y=kx+2k与x2+y2+mx=0都有公共点”的充要条件,故③错误;
由$\frac{{S}_{△PAB}}{\overrightarrow{PA}•\overrightarrow{PB}}$=$\frac{{S}_{△PBC}}{\overrightarrow{PB}•\overrightarrow{PC}}$=$\frac{{S}_{△PAC}}{\overrightarrow{PA}•\overrightarrow{PC}}$,
可得tan∠APB=tan∠BPC=tan∠APC,
由于0<∠APB,∠BPC,∠APC<π,且∠APB+∠BPC+∠APC=2π,
则∠APB=∠BPC=∠APC=$\frac{2π}{3}$,
由于AB=AC=3,BC=2,
由△APB≌△APC,
则PB=PC=$\frac{2\sqrt{3}}{3}$,
在△APB中,AB2=AP2+BP2-2AP•BPcos$\frac{2π}{3}$,
即有9=AP2+$\frac{4}{3}$+$\frac{2\sqrt{3}}{3}$AP,
解得AP=-$\frac{\sqrt{3}}{3}$+2$\sqrt{2}$,
则有PA+PB+PC=2$\sqrt{2}$+$\sqrt{3}$,故④正确;
故答案为:②④
点评 本题以命题的真假判断与应用为载体,考查了特称命题的否定,直线与圆的位置关系,空间直线与平面的位置关系,平面向量在几何中的应用等知识点,难度中档.


科目:高中数学 来源: 题型:选择题

| A. | (-∞,0) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
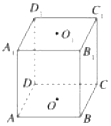 如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.
如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+1 | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\frac{\sqrt{3}}{2}$+1 | D. | $\frac{\sqrt{3}-1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的几何体中,四边形DCFE为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,且AC⊥FB.
在如图所示的几何体中,四边形DCFE为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,且AC⊥FB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\sqrt{x}$>1,则lnx≤0 | B. | 若$\sqrt{x}$≤1,则lnx>0 | C. | 若$\sqrt{x}$≤1,则lnx≤0 | D. | 若lnx>0,则$\sqrt{x}$>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com