
【题目】已知函数f(x)=loga ![]() (a>0且a≠1)是奇函数.
(a>0且a≠1)是奇函数.
(1)求实数m的值;
(2)判断函数f(x)在区间(1,+∞)上的单调性并说明理由;
(3)当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞),求实数n,a的值.
【答案】
(1)解:根据题意,函数f(x)=loga![]() (a>0且a≠1)是奇函数,
(a>0且a≠1)是奇函数,
则有f(x)+f(﹣x)=0,
即loga![]() +loga
+loga![]() =0,
=0,
则有loga( ![]() )(
)( ![]() )=0,
)=0,
即( ![]() )(
)( ![]() )=1,
)=1,
解可得:m=±1,
当m=1时,f(x)=loga![]() ,没有意义,
,没有意义,
故m=﹣1
(2)解:由(1)可得:m=﹣1,即f(x)=loga![]() ,
,
设x1>x2>1,
f(x1)﹣f(x2)=loga![]() ﹣loga
﹣loga![]() =loga
=loga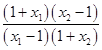 =loga(
=loga( ![]() ),
),
又由x1>x2>1,
则0< ![]() <1,
<1,
当a>1时,f(x1)﹣f(x2)<0,则函数f(x)为减函数,
当0<a<1时,f(x1)﹣f(x2)>0,则函数f(x)为增函数
(3)解:由(1)可得:m=﹣1,即f(x)=loga![]() ,
,
其定义域为(﹣∞,﹣1)∪(1,+∞),
当n<a﹣2<﹣1时,有0<a<1,
此时函数f(x)为增函数,有 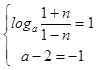 ,无解;
,无解;
当1<n<a﹣2时,有a﹣2>1,即a>3,
此时函数f(x)为减函数,有 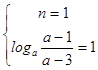 ,解可得a=2+
,解可得a=2+ ![]() ;
;
故n=1,a=2+ ![]()
【解析】(1)根据题意,由函数奇偶性的性质可得f(x)+f(﹣x)=0,即loga ![]() +loga
+loga ![]() =0,结合对数的运算性质可得(
=0,结合对数的运算性质可得( ![]() )(
)( ![]() )=1,解可得m的值,验证即可得答案;(2)由(1)可得函数的解析式,设x1>x2>1,结合对数的运算性质可得f(x1)﹣f(x2)=loga(
)=1,解可得m的值,验证即可得答案;(2)由(1)可得函数的解析式,设x1>x2>1,结合对数的运算性质可得f(x1)﹣f(x2)=loga( ![]() ),分a>1与0<a<1两种情况讨论f(x1)﹣f(x2)的符号,综合可得答案;(3)由(1)可得函数的解析式,进而求出函数f(x)的定义域,分n<a﹣2<﹣1和1<n<a﹣2两种情况讨论,求出a、n的值,即可得答案.
),分a>1与0<a<1两种情况讨论f(x1)﹣f(x2)的符号,综合可得答案;(3)由(1)可得函数的解析式,进而求出函数f(x)的定义域,分n<a﹣2<﹣1和1<n<a﹣2两种情况讨论,求出a、n的值,即可得答案.
【考点精析】根据题目的已知条件,利用奇偶性与单调性的综合的相关知识可以得到问题的答案,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系 ![]() 中,过椭圆
中,过椭圆 ![]() :
: ![]() (
( ![]() )右焦点的直线
)右焦点的直线 ![]() 交
交 ![]() 于
于 ![]() ,
, ![]() 两点,
两点, ![]() 为
为 ![]() 的中点,且
的中点,且 ![]() 的斜率为
的斜率为 ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ) ![]() ,
, ![]() 为
为 ![]() 上的两点,若四边形
上的两点,若四边形 ![]() . 的对角线
. 的对角线 ![]() ,求四边形
,求四边形 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E、F分别为A1C1、B1C1的中点,D为棱CC1上任一点. 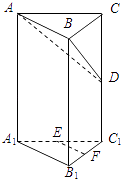
(Ⅰ)求证:直线EF∥平面ABD;
(Ⅱ)求证:平面ABD⊥平面BCC1B1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数, ![]() 为常数.
为常数.
(1)确定![]() 的值;
的值;
(2)求证: ![]() 是
是![]() 上的增函数;
上的增函数;
(3)若对于区间![]() 上的每一个
上的每一个![]() 值,不等式
值,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种新型的洗衣液,去污速度特别快.已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟) 变化的函数关系式近似为
(分钟) 变化的函数关系式近似为![]() ,其中
,其中 .根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
(1)若投放![]() 个单位的洗衣液,3分钟时水中洗衣液的浓度为4 (克/升),求
个单位的洗衣液,3分钟时水中洗衣液的浓度为4 (克/升),求![]() 的值;
的值;
(2)若投放4个单位的洗衣液,则有效去污时间可达几分钟?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD的体积为![]() ,其三视图如图所示,其中正视图为等腰三角形,侧视图为直角三角形,俯视图是直角梯形.
,其三视图如图所示,其中正视图为等腰三角形,侧视图为直角三角形,俯视图是直角梯形.

(1)求正视图的面积;
(2)求四棱锥P-ABCD的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足:
满足: ![]() ,且该函数的最小值为1.
,且该函数的最小值为1.
(1)求此二次函数![]() 的解析式;
的解析式;
(2)若函数![]() 的定义域为
的定义域为![]() (其中
(其中![]() ),问是否存在这样的两个实数
),问是否存在这样的两个实数![]() ,
, ![]() ,使得函数
,使得函数![]() 的值域也为
的值域也为![]() ?若存在,求出
?若存在,求出![]() ,
, ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若对于任意的![]() ,总存在
,总存在![]() 使得
使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com