
【题目】在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E、F分别为A1C1、B1C1的中点,D为棱CC1上任一点. 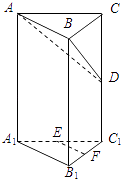
(Ⅰ)求证:直线EF∥平面ABD;
(Ⅱ)求证:平面ABD⊥平面BCC1B1 .
【答案】证明:(Ⅰ)因为E、F分别为A1C1,B1C1的中点,所以EF∥A1B1∥AB
而EF面ABD,AB面ABD,所以直线EF∥平面ABD
(Ⅱ)因为三棱柱ABC﹣A1B1C1为直三棱柱,所以AB⊥BB1,又AB⊥BC,
而BB1面BCC1B1,BC面BCC1B1,且BB1∩BC=B,所以AB⊥面BCC1B1
又AB面ABD,所以平面ABD⊥平面BCC1B1
【解析】(I)因为E、F分别为A1C1,B1C1的中点,由三角形中位线定理,我们易证明EF∥AB,根据线面平行的判定定理,我们易得直线EF∥平面ABD;(Ⅱ)由已知中直三棱柱ABC﹣A1B1C1中,∠ABC=90°,结合线面垂直判定定理,我们易得AB⊥面BCC1B1,再由面面垂直判定定理,即可得到平面ABD⊥平面BCC1B1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设U=R,A={x|x≤2,或x≥5},B= ![]() ,C={x|a<x<a+1}
,C={x|a<x<a+1}
(1)求A∪B和(UA)∩B
(2)若B∩C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() ,且与
,且与![]() 轴有唯一的交点
轴有唯一的交点![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)设函数![]() ,若
,若![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,记此函数的最小值为
,记此函数的最小值为![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】锐角△ABC中,角A、B、C所对的边分别为a、b、c,且tanA﹣tanB= ![]() (1+tanAtanB). (Ⅰ)若c2=a2+b2﹣ab,求角A、B、C的大小;
(1+tanAtanB). (Ⅰ)若c2=a2+b2﹣ab,求角A、B、C的大小;
(Ⅱ)已知向量 ![]() =(sinA,cosA),
=(sinA,cosA), ![]() =(cosB,sinB),求|3
=(cosB,sinB),求|3 ![]() ﹣2
﹣2 ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:①
点,则翻折后的几何体中有如下描述:①![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;②
;②![]() ;③
;③![]() ;④平面
;④平面![]() 平面
平面![]() ,其中正确的命题序号为___________.
,其中正确的命题序号为___________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() (a>0且a≠1)是奇函数.
(a>0且a≠1)是奇函数.
(1)求实数m的值;
(2)判断函数f(x)在区间(1,+∞)上的单调性并说明理由;
(3)当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞),求实数n,a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
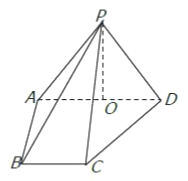
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,侧棱
,侧棱![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]() 为
为![]() 中点.
中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)线段![]() 上是否存在
上是否存在![]() ,使得它到平面
,使得它到平面![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com