
【题目】已知f(x)= ![]() ,若不等式
,若不等式 ![]() 对任意的
对任意的 ![]() 恒成立,则整数λ的最小值为 .
恒成立,则整数λ的最小值为 .
【答案】1
【解析】解:∵f(x)= ![]() ,
,
令f(x)>﹣ ![]() ,
,
解得:x> ![]() ,
,
若对任意θ∈[0, ![]() ],不等式f(cos2θ+λsinθ﹣
],不等式f(cos2θ+λsinθ﹣ ![]() )+
)+ ![]() ≥0恒成立,
≥0恒成立,
则对任意θ∈[0, ![]() ],cos2θ+λsinθ﹣
],cos2θ+λsinθ﹣ ![]() ≥
≥ ![]() 恒成立,
恒成立,
即1﹣sin2θ+λsinθ﹣ ![]() ≥
≥ ![]() 恒成立,
恒成立,
当θ=0时,不等式恒成立,
当θ≠0时,1﹣sin2θ+λsinθ﹣ ![]() ≥
≥ ![]() 可化为:λ≥
可化为:λ≥ ![]() =sinθ﹣
=sinθ﹣ ![]() ,
,
当θ= ![]() 时,sinθ﹣
时,sinθ﹣ ![]() 取最大值
取最大值 ![]() ,
,
故λ> ![]() ,
,
故整数λ的最小值为1,
故答案为:1.
令f(x)>﹣ ![]() ,解得:x>
,解得:x> ![]() ,若对任意θ∈[0,
,若对任意θ∈[0, ![]() ],不等式f(cos2θ+λsinθ﹣
],不等式f(cos2θ+λsinθ﹣ ![]() )+
)+ ![]() ≥0恒成立,则对任意θ∈[0,
≥0恒成立,则对任意θ∈[0, ![]() ],cos2θ+λsinθ﹣
],cos2θ+λsinθ﹣ ![]() ≥
≥ ![]() 恒成立,进而得到答案.
恒成立,进而得到答案.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知实数x1 , x2 , x3 , x4 , x5满足0<x1<x2<x3<x4<x5
(1)求证不等式x12+x22+x32+x42+x52>x1x2+x2x3+x3x4+x4x5+x5x1
(2)随机变量X取值 ![]() 的概率均为
的概率均为 ![]() ,随机变量Y取值
,随机变量Y取值 ![]() 的概率也均为
的概率也均为 ![]() ,比较DX与DY大小关系.
,比较DX与DY大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某商品在过去的100天内的销售量(单位:件)和价格(单位:元)均为时间![]() (单位:天)的函数,且销售量满足
(单位:天)的函数,且销售量满足![]() =
=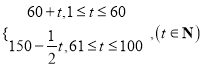 ,价格满足
,价格满足![]() =
=![]() .
.
(1)求该种商品的日销售额![]() 与时间
与时间![]() 的函数关系;
的函数关系;
(2)若销售额超过16610元,商家认为该商品的收益达到理想程度,请判断该商品在哪几天的收益达到理想程度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E、F分别为A1C1、B1C1的中点,D为棱CC1上任一点. 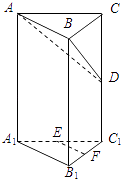
(Ⅰ)求证:直线EF∥平面ABD;
(Ⅱ)求证:平面ABD⊥平面BCC1B1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M,N分别是A1B,B1C1的中点.
(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成的角的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com