
【题目】已知函数![]() 是偶函数,且
是偶函数,且![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 在
在![]() 上的值域.
上的值域.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由偶函数定义知![]() 恒成立,由此可求
恒成立,由此可求![]() ,由
,由![]() 可求
可求![]() ;(2)根据图象平移可得
;(2)根据图象平移可得![]() 的解析式,根据二次函数的性质可求值域.
的解析式,根据二次函数的性质可求值域.
试题解析:(1)![]() 是偶函数
是偶函数
![]()
又![]()
![]()
![]()
(2)由(1)知, ![]()
![]() ,即函数
,即函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
当![]() 时,有
时,有![]() ;
;
当![]() 时,有
时,有![]() .
.
∴函数![]() 在
在![]() 上的值域为
上的值域为![]() .
.
点睛:本题考查求函数的解析式,函数的值域. 二次函数在闭区间上必有最大值和最小值,它只能在区间的端点或二次函数图象的顶点处取到;常见题型有:(1)轴固定区间也固定;(2)轴动(轴含参数),区间固定;(3)轴固定,区间动(区间含参数). 找最值的关键是:(1)图象的开口方向;(2)对称轴与区间的位置关系;(3)结合图象及单调性确定函数最值.


科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C极坐标方程: ![]() ,点P极坐标为
,点P极坐标为 ![]() ,直线l过点P,且倾斜角为
,直线l过点P,且倾斜角为 ![]() .
.
(1)求曲线C的直角坐标方程及直线l参数方程;
(2)若直线l与曲线C交于A,B两点,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() (a>0)
(a>0)
(1)若函数f(x)在x=2处的切线与x轴平行,求实数a的值;
(2)讨论函数f(x)在区间[1,2]上的单调性;
(3)证明: ![]() >e.
>e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】( 本小题满分14)
如图,在三棱锥P—ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.
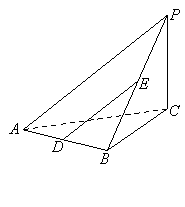
(1)求证:DE∥平面PAC
(2)求证:AB⊥PB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是
是![]() 直径,
直径, ![]() 所在的平面,
所在的平面, ![]() 是圆周上不同于
是圆周上不同于![]() 的动点.
的动点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,且当二面角
,且当二面角![]() 的正切值为
的正切值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点.
的中点.
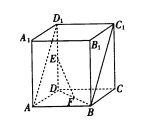
(1)求证: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com