
【题目】已知函数f(x)=lnx﹣ ![]() (a>0)
(a>0)
(1)若函数f(x)在x=2处的切线与x轴平行,求实数a的值;
(2)讨论函数f(x)在区间[1,2]上的单调性;
(3)证明: ![]() >e.
>e.
【答案】
(1)解:∵ ![]() ,(x>0)
,(x>0)
∵函数f(x)在x=2处的切线与x轴平行
∴f′(2)= ![]() ,解得a=
,解得a= ![]()
(2)解:∵ ![]() =
= ![]() ,(x>0,a>0)
,(x>0,a>0)
令h(x)=ax2+(2a﹣2)x+a,(a>0),△=4﹣8a
①)当△=4﹣8a≤0,即a ![]() 时,f′(x)≥0在(0,+∞)恒成立,此时函数f(x)在区间[1,2]上单调递增;
时,f′(x)≥0在(0,+∞)恒成立,此时函数f(x)在区间[1,2]上单调递增;
②当△=4﹣8a>0,即0<a ![]() 时,抛物线y=ax2+(2a﹣2)x+a的图象如下,与横轴交点横坐标为x1=
时,抛物线y=ax2+(2a﹣2)x+a的图象如下,与横轴交点横坐标为x1= ![]() ,x2=
,x2= ![]()
h(1)=4a﹣2<0,h(2)=9a﹣4
当h(2)=9a﹣4≤0,即0 ![]() 时,h(x)≤0在(1,2)上恒成立,∴f′(x)≤0在(1,2)上恒成立,此时函数f(x)在区间[1,2]上单调递减
时,h(x)≤0在(1,2)上恒成立,∴f′(x)≤0在(1,2)上恒成立,此时函数f(x)在区间[1,2]上单调递减
当h(2)=9a﹣4<0,即 ![]() 时,h(x)≤0在(1,x2)上恒成立,h(x)≥0在(x2,2)上恒成立,此时函数f(x)在区间[1,
时,h(x)≤0在(1,x2)上恒成立,h(x)≥0在(x2,2)上恒成立,此时函数f(x)在区间[1, ![]() ]上单调递减
]上单调递减
,在( ![]() ,2)上单调递增
,2)上单调递增
(3)证明:由(2)可知,当a=0.5时,函数f(x)在区间[1,2]上单调递增;即lnx ![]() 在区间[1,2]上恒成立.
在区间[1,2]上恒成立.
令x=1+ ![]() ,(n∈N+),则有ln(1+
,(n∈N+),则有ln(1+ ![]() )>
)> 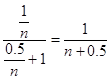
(n+0.5)ln ![]() >1ln(
>1ln( ![]() )n+0.5>1
)n+0.5>1 ![]() ,
,
令n=2017,可得 ![]() >e
>e
【解析】(1) ![]() ,(x>0)由f′(2)=
,(x>0)由f′(2)= ![]() ,解得a(2)
,解得a(2) ![]() =
= ![]() ,(x>0,a>0),令h(x)=ax2+(2a﹣2)x+a,(a>0),△=4﹣8a,分①)当△=4﹣8a≤0,即a
,(x>0,a>0),令h(x)=ax2+(2a﹣2)x+a,(a>0),△=4﹣8a,分①)当△=4﹣8a≤0,即a ![]() 时,②当△=4﹣8a>0,即0<a
时,②当△=4﹣8a>0,即0<a ![]() 讨论;(3)由(2)可知,当a=0.5时,函数f(x)在区间[1,2]上单调递增;即lnx
讨论;(3)由(2)可知,当a=0.5时,函数f(x)在区间[1,2]上单调递增;即lnx ![]() 在区间[1,2]上恒成立,令x=1+
在区间[1,2]上恒成立,令x=1+ ![]() ,(n∈N+),则有ln(1+
,(n∈N+),则有ln(1+ ![]() )>
)> 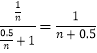 (n+0.5)ln
(n+0.5)ln ![]() >1ln(
>1ln( ![]() )n+0.5>1
)n+0.5>1 ![]() ,令n=2017,可得
,令n=2017,可得 ![]() >e.
>e.
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.极坐标系中方程ρ2﹣4ρcosθ=0和ρ﹣4cosθ=0表示的是同一曲线
B.![]()
C.不等式|a+b|≥|a|﹣|b|等号成立的条件为ab≤0
D.在极坐标系中方程 ![]() 表示的圆和一条直线.
表示的圆和一条直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的方程为
的方程为 ![]() ,直线
,直线 ![]() 的倾斜角为
的倾斜角为 ![]() 且经过点
且经过点 ![]() .
.
(1)以 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线 ![]() 的极坐标方程;
的极坐标方程;
(2)设直线 ![]() 与曲线
与曲线 ![]() 交于两点
交于两点 ![]() ,
, ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为R
的定义域为R
(1)当a=2时,求函数f(x)的值域
(2)若函数f(x)是奇函数,①求a的值;②解不等式f(3﹣m)+f(3﹣m2)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某商品在过去的100天内的销售量(单位:件)和价格(单位:元)均为时间![]() (单位:天)的函数,且销售量满足
(单位:天)的函数,且销售量满足![]() =
=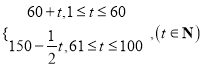 ,价格满足
,价格满足![]() =
=![]() .
.
(1)求该种商品的日销售额![]() 与时间
与时间![]() 的函数关系;
的函数关系;
(2)若销售额超过16610元,商家认为该商品的收益达到理想程度,请判断该商品在哪几天的收益达到理想程度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个定点![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率;
的斜率;
(3)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点.
是否过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com