
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点.
的中点.
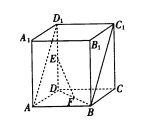
(1)求证: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)连接BD1,由中位线定理证明EF∥D1B,由线面平行的判定定理证明EF∥平面ABC1D1;
(2)由(1)和异面直线所成角的定义,得异面直线EF与BC所成的角是∠D1BC,由题意和球的表面积公式求出外接球的半径,由勾股定理求出侧棱AA1的长,由直四棱柱的结构特征和线面垂直的定义,判断出BC⊥CD1,在RT△CC1D1中求出tan∠D1BC,求出∠D1BC可得答案.
试题解析:
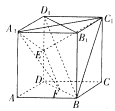
(1)连接![]() ,在
,在![]() 中,
中, ![]() 分别为线段
分别为线段![]() 的中点,∴
的中点,∴![]() 为中位线,
为中位线,
∴![]() ,而
,而![]() 面
面![]() ,
, ![]() 面
面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)由(1)知![]() ,故
,故![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成的角.
所成的角.
∵四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,
,
∴四棱柱![]() 的外接球的半径
的外接球的半径![]() ,
,
设![]() ,则
,则![]() ,解得
,解得![]() ,
,
在直四棱柱![]() 中,∵
中,∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,在
,在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴异面直线![]() 与
与![]() 所成的角为
所成的角为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知两个定点![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率;
的斜率;
(3)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点.
是否过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M,N分别是A1B,B1C1的中点.
(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成的角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,如果存在函数
,如果存在函数![]() ,使得函数
,使得函数![]() 的值域仍是
的值域仍是![]() ,那么称
,那么称![]() 是函数
是函数![]() 的一个等值域变换.
的一个等值域变换.
(1)判断下列函数![]() 是不是函数
是不是函数![]() 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由;
①![]() ;
;
②![]() .
.
(2)设![]() 的定义域为
的定义域为![]() ,已知
,已知![]() 是
是![]() 的一个等值域变换,且函数
的一个等值域变换,且函数![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电台在因特网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12000人,其中持各种态度的人数如下表:
很喜爱 | 喜爱 | 一般 | 不喜爱 |
2435 | 4567 | 3926 | 1072 |
电视台为进一步了解观众的具体想法和意见,打算从中抽取60人进行更为详细的调查,应当怎样进行抽样?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x+b)ex , F(x)=bx﹣lnx,b∈R.
(1)若b<0,且存在区间M,使f(x)和F(x)在区间M上具有相同的单调性,求b的取值范围;
(2)若F(x+1)>b对任意x∈(0,+∞)恒成立,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com