
【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C极坐标方程: ![]() ,点P极坐标为
,点P极坐标为 ![]() ,直线l过点P,且倾斜角为
,直线l过点P,且倾斜角为 ![]() .
.
(1)求曲线C的直角坐标方程及直线l参数方程;
(2)若直线l与曲线C交于A,B两点,求 ![]() .
.
【答案】
(1)解:∵曲线C极坐标方程: ![]() ,∴3ρ2+ρ2sin2θ=12,
,∴3ρ2+ρ2sin2θ=12,
∵ρ2=x2+y2,ρsinθ=y,
∴曲线C的直角坐标方程为3x2+4y2=12,即 ![]() =1.
=1.
∵点P极坐标为 ![]() ,直线l过点P,且倾斜角为
,直线l过点P,且倾斜角为 ![]() .
.
∴点P的直角坐标为(3, ![]() ),
),
∴直线l参数方程为 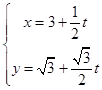 (t为参数)
(t为参数)
(2)解:把直线l参数方程 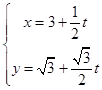 (t为参数)代入曲线C:3x2+4y2=12,
(t为参数)代入曲线C:3x2+4y2=12,
整理,得: ![]() ,
,
![]() =4>0,
=4>0,
设方程的两根为t1,t2,则t1+t2=﹣ ![]() ,t1t2=
,t1t2= ![]() ,∴t1<0,t2<0,
,∴t1<0,t2<0,
∴ 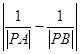 =|
=| ![]() |=|
|=| 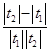 |=
|= 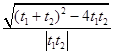 =
= 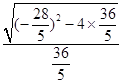 =
= ![]()
【解析】(1)曲线C极坐标方程转化为3ρ2+ρ2sin2θ=12,由ρ2=x2+y2,ρsinθ=y,能求出曲线C的直角坐标方程;由直线l过点P(3, ![]() ),且倾斜角为
),且倾斜角为 ![]() ,能求出直线l参数方程.(2)把直线l参数方程
,能求出直线l参数方程.(2)把直线l参数方程 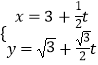 (t为参数)代入曲线C:3x2+4y2=12,得:
(t为参数)代入曲线C:3x2+4y2=12,得: ![]() ,由此利用韦达定理,结合已知条件能求出
,由此利用韦达定理,结合已知条件能求出 ![]() 的值.
的值.


科目:高中数学 来源: 题型:
【题目】定义:已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,若
,若![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上具有“
上具有“![]() ”性质.
”性质.
(![]() )判断函数
)判断函数![]() 在
在![]() 上是否具有“
上是否具有“![]() ”性质?说明理由.
”性质?说明理由.
(![]() )若
)若![]() 在
在![]() 上具有“
上具有“![]() ”性质,求
”性质,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市准备在道路![]() 的一侧修建一条运动比赛道,赛道的前一部分为曲线段
的一侧修建一条运动比赛道,赛道的前一部分为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
, ![]() 时的图象,且图象的最高点为
时的图象,且图象的最高点为![]() .赛道的中间部分为长
.赛道的中间部分为长![]() 千米的直线跑道
千米的直线跑道![]() ,且
,且![]() .赛道的后一部分是以
.赛道的后一部分是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.

(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圆弧赛道所对应的扇形![]() 区域内建一个“矩形草坪”,矩形的一边在道路
区域内建一个“矩形草坪”,矩形的一边在道路![]() 上,一个顶点在半径
上,一个顶点在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求当“矩形草坪”的面积取最大值时
,求当“矩形草坪”的面积取最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.极坐标系中方程ρ2﹣4ρcosθ=0和ρ﹣4cosθ=0表示的是同一曲线
B.![]()
C.不等式|a+b|≥|a|﹣|b|等号成立的条件为ab≤0
D.在极坐标系中方程 ![]() 表示的圆和一条直线.
表示的圆和一条直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2|x|.
(1)将函数f(x)写成分段函数;
(2)判断函数的奇偶性,并画出函数图象.
(3)若函数在[a, +∞)上单调,求a的范围。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x1 , x2 , x3 , x4 , x5满足0<x1<x2<x3<x4<x5
(1)求证不等式x12+x22+x32+x42+x52>x1x2+x2x3+x3x4+x4x5+x5x1
(2)随机变量X取值 ![]() 的概率均为
的概率均为 ![]() ,随机变量Y取值
,随机变量Y取值 ![]() 的概率也均为
的概率也均为 ![]() ,比较DX与DY大小关系.
,比较DX与DY大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的方程为
的方程为 ![]() ,直线
,直线 ![]() 的倾斜角为
的倾斜角为 ![]() 且经过点
且经过点 ![]() .
.
(1)以 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线 ![]() 的极坐标方程;
的极坐标方程;
(2)设直线 ![]() 与曲线
与曲线 ![]() 交于两点
交于两点 ![]() ,
, ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com