
【题目】定义:已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,若
,若![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上具有“
上具有“![]() ”性质.
”性质.
(![]() )判断函数
)判断函数![]() 在
在![]() 上是否具有“
上是否具有“![]() ”性质?说明理由.
”性质?说明理由.
(![]() )若
)若![]() 在
在![]() 上具有“
上具有“![]() ”性质,求
”性质,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的可导函数,且满足f′(x)>f(x),对任意的正数a,下面不等式恒成立的是( )
A.f(a)<eaf(0)
B.f(a)>eaf(0)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0 , 则称x0是f(x)的一个不动点.
(1)若函数f(x)=2x+ ![]() ﹣5,求此函数的不动点;
﹣5,求此函数的不动点;
(2)若二次函数f(x)=ax2﹣x+3在x∈(1,+∞)上有两个不同的不动点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 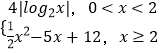 ,若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0,则abcd的取值范围是( )
,若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0,则abcd的取值范围是( )
A.(16,21)
B.(16,24)
C.(17,21)
D.(18,24)
查看答案和解析>>
科目:高中数学 来源: 题型:
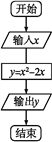
【题目】求函数y=![]() 的值的程序框图如图所示.
的值的程序框图如图所示.
(1)指出程序框图中的错误,并写出算法;
(2)重新绘制解决该问题的程序框图,并回答下面提出的问题.
①要使输出的值为正数,输入的x的值应满足什么条件?
②要使输出的值为8,输入的x值应是多少?
③要使输出的y值最小,输入的x值应是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和所支出的维修费用y(单位:万元)有如下的统计资料:
使用年限x/年 | 2 | 3 | 4 | 5 | 6 |
维修费用y/万元 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系.试求:
(1)回归方程![]() x+
x+![]() 的系数
的系数![]() .
.
(2)使用年限为10年时,试估计维修费用是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段、现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
[60,70) | ① | 0.16 |
[70,80) | 22 | ② |
[80,90) | 14 | 0.28 |
[90,100) | ③ | ④ |
合计 | 50 | 1 |
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)决赛规则如下:参加决赛的每位同学依次口答4道小题,答对2道题就终止答题,并获得一等奖.如果前三道题都答错,就不再答第四题.某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于80分的频率的值相同. ①求该同学恰好答满4道题而获得一等奖的概率;
②记该同学决赛中答题个数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C极坐标方程: ![]() ,点P极坐标为
,点P极坐标为 ![]() ,直线l过点P,且倾斜角为
,直线l过点P,且倾斜角为 ![]() .
.
(1)求曲线C的直角坐标方程及直线l参数方程;
(2)若直线l与曲线C交于A,B两点,求 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com