
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0 , 则称x0是f(x)的一个不动点.
(1)若函数f(x)=2x+ ![]() ﹣5,求此函数的不动点;
﹣5,求此函数的不动点;
(2)若二次函数f(x)=ax2﹣x+3在x∈(1,+∞)上有两个不同的不动点,求实数a的取值范围.
【答案】
(1)解:函数f(x)=2x+ ![]() ﹣5,
﹣5,
由f(x)=x,即x+ ![]() ﹣5=0,
﹣5=0,
即为x2﹣5x+4=0,解得x=1和4,
则此函数的不动点为1,4
(2)解:二次函数f(x)=ax2﹣x+3在x∈(1,+∞)上有两个不同的不动点,
即为ax2﹣2x+3=0在x∈(1,+∞)上有两个不等的实根,
当a>0时,△=4﹣12a>0,且a﹣2+3>0, ![]() >0,解得0<a<
>0,解得0<a< ![]() ;
;
当a<0,由于对称轴x= ![]() <0,在x∈(1,+∞)上没有两个不等的实根,不成立.
<0,在x∈(1,+∞)上没有两个不等的实根,不成立.
综上可得,0<a< ![]() .
.
则实数a的取值范围为(0, ![]() )
)
【解析】(1)由定义可得f(x)=x,解方程即可得到所求不动点;(2)由题意可得ax2﹣2x+3=0在x∈(1,+∞)上有两个不等的实根,讨论a>0或a<0和判别式大于0,对称轴介于x=1的右边,x=1的函数值大于0,解不等式即可得到所求范围.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;
②设有一个回归方程 ![]() ,变量x增加一个单位时,y平均增加3个单位;
,变量x增加一个单位时,y平均增加3个单位;
③线性回归方程 ![]() 必经过点
必经过点 ![]() ;
;
④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.其中错误的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量y和x进行回归分析,得到一组样本数据:(x1 , y1),(x2 , y2),…,(xn , yn),则下列说法中不正确的是( )
A.由样本数据得到的回归方程 ![]() =
= ![]() x+
x+ ![]() 必过样本中心(
必过样本中心( ![]() ,
, ![]() )
)
B.残差平方和越小的模型,拟合的效果越好
C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立坐标系.已知曲线C:ρsin2θ=2acosθ(a>0),过点P(﹣2,﹣4)的直线l的参数方程为 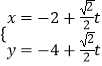 (t为参数),直线l与曲线C分别交于M、N两点.
(t为参数),直线l与曲线C分别交于M、N两点.
(1)写出曲线C和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过市场调查,得到某种产品的资金投入x(单位:万元)与获得的利润y(单位:万元)的数据,如表所示:
资金投入x | 2 | 3 | 4 | 5 | 6 |
利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() x+
x+![]() ;
;
(3)现投入资金10万元,求获得利润的估计值为多少万元?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,若f(x)满足条件:存在[a,b]D,使f(x)在[a,b]上的值域是[ ![]() ,
, ![]() ],则成f(x)为“倍缩函数”,若函数f(x)=log2(2x+t)为“倍缩函数”,则t的范围是( )
],则成f(x)为“倍缩函数”,若函数f(x)=log2(2x+t)为“倍缩函数”,则t的范围是( )
A.(0, ![]() )
)
B.(0,1)
C.(0, ![]() ]
]
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,若
,若![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上具有“
上具有“![]() ”性质.
”性质.
(![]() )判断函数
)判断函数![]() 在
在![]() 上是否具有“
上是否具有“![]() ”性质?说明理由.
”性质?说明理由.
(![]() )若
)若![]() 在
在![]() 上具有“
上具有“![]() ”性质,求
”性质,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一箱方便面共有50袋,用随机抽样方法从中抽取了10袋,并称其质量(单位:g)结果为:60.5 61 60 60 61.5 59.5 59.5 58 60 60
(1)指出总体、个体、样本、样本容量;
(2)指出样本数据的众数、中位数、平均数;
(3)求样本数据的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.极坐标系中方程ρ2﹣4ρcosθ=0和ρ﹣4cosθ=0表示的是同一曲线
B.![]()
C.不等式|a+b|≥|a|﹣|b|等号成立的条件为ab≤0
D.在极坐标系中方程 ![]() 表示的圆和一条直线.
表示的圆和一条直线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com