
����Ŀ����ͼ��ij�����ڵ�·![]() ��һ����һ���˶���������������ǰһ����Ϊ���߶�
��һ����һ���˶���������������ǰһ����Ϊ���߶�![]() �������߶��Ǻ���
�������߶��Ǻ���![]() ��
�� ![]() ʱ��ͼ����ͼ�����ߵ�Ϊ
ʱ��ͼ����ͼ�����ߵ�Ϊ![]() .�������м䲿��Ϊ��
.�������м䲿��Ϊ��![]() ǧ��ֱ���ܵ�
ǧ��ֱ���ܵ�![]() ����
����![]() .�����ĺ�һ��������
.�����ĺ�һ��������![]() ΪԲ�ĵ�һ��Բ��
ΪԲ�ĵ�һ��Բ��![]() .
.

(1)��![]() ��ֵ��
��ֵ��![]() �Ĵ�С��
�Ĵ�С��
(2)��Ҫ��Բ����������Ӧ������![]() �����ڽ�һ�������β�ƺ�������ε�һ���ڵ�·
�����ڽ�һ�������β�ƺ�������ε�һ���ڵ�·![]() �ϣ�һ�������ڰ뾶
�ϣ�һ�������ڰ뾶![]() �ϣ�����һ������
�ϣ�����һ������![]() ��Բ��
��Բ��![]() �ϣ���
�ϣ���![]() ,�����β�ƺ�������ȡ���ֵʱ
,�����β�ƺ�������ȡ���ֵʱ![]() ��ֵ.
��ֵ.
���𰸡���1��![]() ��
�� ![]() ����2��
����2��![]() .
.
�����������������
��1��������ɵ�![]() ����
����![]() ���Ӷ��ɵ����߶�
���Ӷ��ɵ����߶�![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ����x=0�ɵ�
����x=0�ɵ�![]() ������
������![]() ����
����![]() ,���
,���![]() ��2���������ɵõ������β�ƺ����������ʱ����
��2���������ɵõ������β�ƺ����������ʱ����![]() �ڻ�
�ڻ�![]() �ϣ��������ɵá����β�ƺ�������Ϊ
�ϣ��������ɵá����β�ƺ�������Ϊ![]() ��Ȼ�����
��Ȼ�����![]() �ķ�Χ�ɵõ�
�ķ�Χ�ɵõ�![]() ʱ��
ʱ��![]() ȡ�����ֵ��
ȡ�����ֵ��
���������
(1)��������![]() .
.
��![]() .
.
�����߶�![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() .
.
��![]() ʱ��
ʱ��![]() .
.
��![]() ��
��
��![]() ,
,
��![]() .
.
(2)��(1)����֪![]() .
.
����֪�������β�ƺ����������ʱ����![]() �ڻ�
�ڻ�![]() �ϣ���
�ϣ���![]() .
.
��![]() ,
,![]() ,�����β�ƺ�������Ϊ
,�����β�ƺ�������Ϊ
![]()
![]() .
.
��![]() ��
��
��![]() ,
,
�ʵ�![]() ����
����![]() ʱ��
ʱ��![]() ȡ�����ֵ��
ȡ�����ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x���Ƕ�����R�ϵĿɵ�������������f�䣨x����f��x���������������a�����治��ʽ��������ǣ� ��
A.f��a����eaf��0��
B.f��a����eaf��0��
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ij�豸��ʹ������x����֧����ά����y(��λ:��Ԫ)�����µ�ͳ������:
ʹ������x/�� | 2 | 3 | 4 | 5 | 6 |
ά����y/��Ԫ | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
��������֪y��x��������ع�ϵ.����:
(1)�ع鷽��![]() x+
x+![]() ��ϵ��
��ϵ��![]() .
.
(2)ʹ������Ϊ10��ʱ,�Թ���ά�����Ƕ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�༶����һ��֪ʶ����������Ϊ�����;��������Ρ��ֽ���������ɼ����÷־�Ϊ����������Ϊ100�֣�����ͳ�ƣ��Ƴ�����Ƶ�ʷֲ�����
�����������Σ� | Ƶ���������� | Ƶ�� |
[60��70�� | �� | 0.16 |
[70��80�� | 22 | �� |
[80��90�� | 14 | 0.28 |
[90��100�� | �� | �� |
�ϼ� | 50 | 1 |
��1�����Ƶ�ʷֲ����еĿո��ڽ����ֱ��д����Ӧ�ո���ŵĴ𰸣���
��2�������������£��μӾ�����ÿλͬѧ���οڴ�4��С�⣬���2�������ֹ���⣬�����һ�Ƚ������ǰ�����ⶼ������Ͳ��ٴ�����⣮ijͬѧ���������ÿ�����Եĸ���P��ֵǡ����Ƶ�ʷֲ����в�����80�ֵ�Ƶ�ʵ�ֵ��ͬ�� �����ͬѧǡ�ô���4��������һ�Ƚ��ĸ��ʣ�
�ڼǸ�ͬѧ�����д������ΪX����X�ķֲ��м���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣
��1���ĸ���ͬ�������Ϊ1��2��3��4���ĸ����У���ǡ��һ���պеķŷ��ж����֣�
��2�����б��Ϊ1��2��3��4��5�������ͱ��Ϊ1��2��3��4��5�ĺ����ֽ���5����Ͷ��5������Ҫ��ÿ�����ӷ�һ������ǡ����������ĺ�������Ӻ�����ͬ�����ж����ֲ�ͬ�ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��5|��|x��2|��
��1����x��R��ʹ��f��x����m��������m�ķ�Χ��
��2����ʽx2��8x+15+f��x����0�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
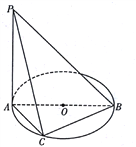
����Ŀ����ͼ�� ![]() ��
��![]() ֱ����
ֱ���� ![]() ���ڵ�ƽ�棬
���ڵ�ƽ�棬 ![]() ��Բ���ϲ�ͬ��
��Բ���ϲ�ͬ��![]() �Ķ���.
�Ķ���.
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ���ҵ������
���ҵ������![]() ������ֵΪ
������ֵΪ![]() ʱ����ֱ��
ʱ����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɵĽǵ�����ֵ.
���ɵĽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У�������ԭ��OΪ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ������C�����귽�̣� ![]() ����P������Ϊ
����P������Ϊ ![]() ��ֱ��l����P������б��Ϊ
��ֱ��l����P������б��Ϊ ![]() ��
��
��1��������C��ֱ�����귽�̼�ֱ��l�������̣�
��2����ֱ��l������C����A��B���㣬�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1���жϺ���![]() ����ż�ԣ�
����ż�ԣ�
��2���жϲ�֤��![]() )��
)��![]() ���ϵĵ����ԣ�
���ϵĵ����ԣ�
��3����![]() ������
������![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com