练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如下图，

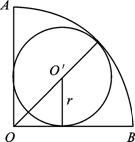
    在扇形AOB中，∠AOB=90°，弧AB长为l，求此扇形内切圆的面积.

    解析：∵弧AB长为l，∠AOB=，

    ∴OA==(+1)r.

    ∴r=(-1).

    ∴S=πr2= l2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如下图，扇形AOB的半径为1，中心角为60°，PQRS是扇形的内接矩形.问P在什么位置时，矩形PQRS的面积最大？试求出这个最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图，“十字形”公路的交叉处周围呈扇形形状，某市规划处拟在这块扇形土地上修建一个圆形广场.怎样设计，广场的占地面积最大，其值是多少？(图中∠AOB=60°，=100π m)

    查看答案和解析>>

    科目：高中数学 来源：四川省绵阳南山中学09-10学年高一下学期期中考试 题型：解答题

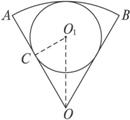
     我校第一学术厅房顶平面成圆心角为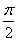的扇形（如下图扇形AOB所示,其中OA=10米）.为了节约能源，提倡低碳，学校计划在第一学术厅房顶平面上水平铺设世博会专用的太阳能屋面(形状如下图矩形阴影部分所示,矩形DOEC的邻边OD、OE分别在OA、OB上,动点C在上),请问动点C在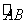上什么位置才能使平铺在房顶的矩形太阳能屋面的面积最大,最大面积是多少？说明理由．   

     

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案