
已知椭圆 的方程为
的方程为 ,双曲线
,双曲线 的左、右焦点分别是
的左、右焦点分别是 的左、右顶点,而
的左、右顶点,而 的
的
左、右顶点分别是 的左、右焦点.
的左、右焦点.
(1)求双曲线 的方程;
的方程;
(2)若直线 与双曲线
与双曲线 恒有两个不同的交点A和B,且
恒有两个不同的交点A和B,且 (其中
(其中 为原点),求实数
为原点),求实数 的范围.
的范围.
(1)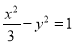 ;(2)
;(2)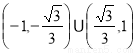
【解析】
试题分析:(1)设双曲线的方程,用待定系数法求出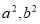 的值;(2)解决直线和双曲线的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与双曲线的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
的值;(2)解决直线和双曲线的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与双曲线的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式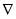 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:【解析】
(1)设双曲线 的方程为
的方程为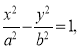
则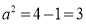 ,再由
,再由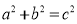 得
得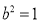
故 的方程为
的方程为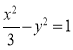
(2)将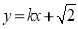 代入
代入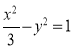
得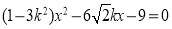
由直线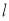 与双曲线C2交于不同的两点得:
与双曲线C2交于不同的两点得:
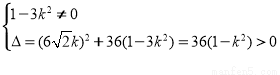
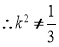 且
且 ①
①
设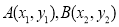 ,则
,则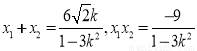
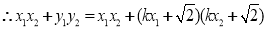
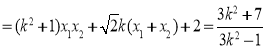
又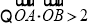 ,得
,得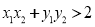
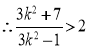
即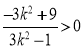 ,解得:
,解得: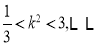 ②
②
由①、②得: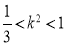
故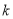 的取值范围为
的取值范围为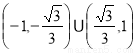
考点:1、求双曲线的方程;2、直线与双曲线的综合问题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源:2015届内蒙古巴彦淖尔市高三10月月考文科数学试卷(解析版) 题型:选择题
已知O、A、B是平面上的三个点,直线AB上有一点C,满足2+= ,则等于( )
,则等于( )
A.2- B.-+2 C.- D.-+
查看答案和解析>>
科目:高中数学 来源:2015届云南省高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
如图,四面体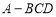 中,
中, ,
, ,平面
,平面 平面
平面 ,若四面体
,若四面体 的四个顶点在同一个球面上,则该球的体积为( )
的四个顶点在同一个球面上,则该球的体积为( )

A.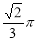 B.
B.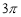 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届云南省高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
一个几何体的三视图如图所示,已知这个几何体的体积为 ,则
,则 的值为( )
的值为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com