
已知函数 (e为自然对数的底数)
(e为自然对数的底数)
(1)求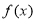 的最小值;
的最小值;
(2)若对于任意的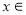
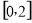 ,不等式
,不等式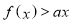 恒成立,求实数
恒成立,求实数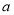 的取值范围.
的取值范围.
(1) 的最小值为1;(2)实数
的最小值为1;(2)实数 的取值范围是
的取值范围是 .
.
【解析】
试题分析:(1)先对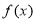 求导,得出函数的单调区间,即可求出函数的最小值为1;
求导,得出函数的单调区间,即可求出函数的最小值为1;
(2)不等式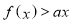 恒成立,变形为
恒成立,变形为 ,构造新函数
,构造新函数 ;求得
;求得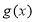 的最小值
的最小值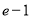 ,
,
从而实数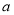 的取值范围是
的取值范围是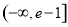 .
.
试题解析:(1) 的导函数
的导函数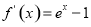 ,令
,令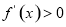 ,解得
,解得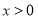 ;
;
令 ,解得
,解得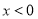 .
.
从而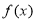 在
在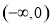 内单调递减,在
内单调递减,在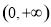 内单调递增.
内单调递增.
所以,当 时,
时,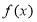 取得最小值1. 6分
取得最小值1. 6分
(2)因为不等式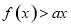 的解集为
的解集为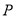 ,且
,且 ,
,
所以对于任意 ,不等式
,不等式 恒成立.
恒成立.
由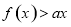 ,得
,得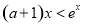 .
.
当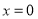 时,上述不等式显然成立,故只需考虑
时,上述不等式显然成立,故只需考虑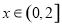 的情况.
的情况.
将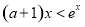 变形为
变形为 .
.
令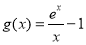 ,则
,则 的导函数
的导函数 ,
,
令 ,解得
,解得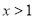 ;令
;令 ,解得
,解得 .
.
从而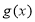 在
在 内单调递减,在
内单调递减,在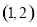 内单调递增.
内单调递增.
所以,当 时,
时,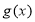 取得最小值
取得最小值 ,
,
从而实数 的取值范围是
的取值范围是 . 13分
. 13分
考点:导函数的综合应用、函数与方程思想.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第3课时练习卷(解析版) 题型:填空题
已知直线x+ay=2a+2与直线ax+y=a+1平行,则实数a的值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:解答题
已知曲线E:ax2+by2=1(a>0,b>0),经过点M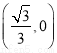 的直线l与曲线E交于点A、B,且
的直线l与曲线E交于点A、B,且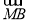 =-2
=-2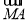 .
.
(1)若点B的坐标为(0,2),求曲线E的方程;
(2)若a=b=1,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练理数学卷(解析版) 题型:填空题
已知平面向量 ,
, ,
, 不共线,且两两之间的夹角都为
不共线,且两两之间的夹角都为 ,若|
,若| |=2,|
|=2,| |=2,|
|=2,| |=1,则
|=1,则 +
+ +
+ 与
与 的夹角是___________.
的夹角是___________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练文数学卷(解析版) 题型:选择题
 分别是双曲线
分别是双曲线 的左右焦点,过点
的左右焦点,过点 的直线
的直线 与双曲线的左右两支分别交于
与双曲线的左右两支分别交于 两点。若
两点。若 是等边三角形,则该双曲线的离心率为( )
是等边三角形,则该双曲线的离心率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安铁一中国际合作学校高三下第一次模拟考试理科数学试卷(解析版) 题型:填空题
设函数 的定义域为
的定义域为 ,若对于给定的正数k, 定义函数
,若对于给定的正数k, 定义函数
 则当函数
则当函数 时,定积分
时,定积分 的值为
的值为
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高考前30天数学保温训练8数列(解析版) 题型:选择题
若f(x)=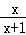 ,则f(1)+f(2)+f(3)…+f(2011)+f(
,则f(1)+f(2)+f(3)…+f(2011)+f( )+f(
)+f( )+…+f(
)+…+f(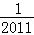 )=( )
)=( )
A.2009 B.2010 C.2012 D.1
C.2012 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com