
已知曲线E:ax2+by2=1(a>0,b>0),经过点M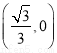 的直线l与曲线E交于点A、B,且
的直线l与曲线E交于点A、B,且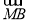 =-2
=-2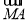 .
.
(1)若点B的坐标为(0,2),求曲线E的方程;
(2)若a=b=1,求直线AB的方程.
(1)x2+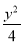 =1(2)y=
=1(2)y= x-1.
x-1.
【解析】(1)设A(x0,y0),由已知B(0,2),M(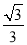 ,0),所以
,0),所以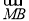 =
= ,
,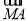 =(x0-
=(x0-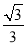 ,y0).
,y0).
由于 =-2
=-2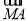 ,所以(-
,所以(-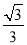 ,2)=-2(x0-
,2)=-2(x0- ,y0),所以
,y0),所以 即A(
即A(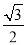 ,-1),将A、B点的坐标代入曲线E的方程,得
,-1),将A、B点的坐标代入曲线E的方程,得 解得
解得
所以曲线E的方程为x2+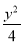 =1.
=1.
(2)当a=b=1时,曲线E为圆x2+y2=1,设A(x1,y1),B(x2,y2).又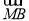 =-2
=-2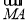 ,
,
所以 =-2(x1-
=-2(x1-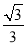 ,y1),
,y1),
即有
 +
+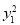 =1①,
=1①,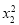 +
+ =1②,由①×4-②,得(2x1+x2)(2x1-x2)=3,所以2x1-x2=
=1②,由①×4-②,得(2x1+x2)(2x1-x2)=3,所以2x1-x2=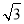 ,解得x1=
,解得x1=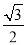 ,x2=0.由x1=
,x2=0.由x1=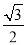 ,得y1=±
,得y1=± .当A
.当A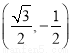 时,B(0,-1),此时kAB=-
时,B(0,-1),此时kAB=- ,直线AB的方程为y=-
,直线AB的方程为y=- x+1;
x+1;
当A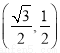 时,B(0,1),此时kAB=
时,B(0,1),此时kAB= ,直线AB的方程为y=
,直线AB的方程为y= x-1.
x-1.


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第4课时练习卷(解析版) 题型:解答题
求过两点A(1,4)、B(3,2)且圆心在直线y=0上的圆的标准方程,并判断点P(2,4)与圆的关系.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:解答题
如图,椭圆E: =1(a>b>0)的左焦点为F1,右焦点为F2,离心率e=
=1(a>b>0)的左焦点为F1,右焦点为F2,离心率e= .过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.

(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:填空题
若双曲线 =1(a>0,b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶3的两段,则此双曲线的离心率为________.
=1(a>0,b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶3的两段,则此双曲线的离心率为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:解答题
已知椭圆C: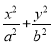 =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:填空题
直线y=kx-k+1与椭圆 =1的位置关系是________.
=1的位置关系是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练理数学卷(解析版) 题型:填空题
以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsin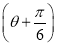 +m=0,曲线C2的参数方程为
+m=0,曲线C2的参数方程为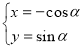 (0<α<π),若曲线C1与C2有两个不同的交点,则实数m的取值范围是____________.
(0<α<π),若曲线C1与C2有两个不同的交点,则实数m的取值范围是____________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练文数学卷(解析版) 题型:解答题
已知函数 (e为自然对数的底数)
(e为自然对数的底数)
(1)求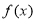 的最小值;
的最小值;
(2)若对于任意的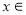
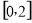 ,不等式
,不等式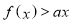 恒成立,求实数
恒成立,求实数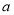 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安铁一中国际合作学校高三下第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知函数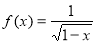 的定义域为
的定义域为 ,
,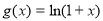 的定义域为
的定义域为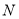 ,则
,则
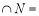 ( )
( )
A.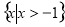 B.
B.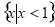 C.
C. D.
D.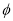
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com