
如图,椭圆E: =1(a>b>0)的左焦点为F1,右焦点为F2,离心率e=
=1(a>b>0)的左焦点为F1,右焦点为F2,离心率e= .过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.

(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
(1)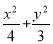 =1(2)存在定点M(1,0),
=1(2)存在定点M(1,0),
【解析】学生错【解析】
【解析】
(1)略
(2)由 消去y得(4k2+3)x2+8kmx+4m2-12=0.
消去y得(4k2+3)x2+8kmx+4m2-12=0.
因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.(*)
此时x0=-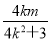 =-
=-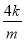 ,y0=kx0+m=
,y0=kx0+m=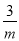 ,所以P
,所以P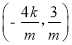 .
.
由 得Q(4,4k+m).
得Q(4,4k+m).
假设平面内存在定点M满足条件,由图形对称性知,点M必在x轴上.
设M(x1,0),则 ·
·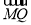 =0对满足(*)式的m,k恒成立.
=0对满足(*)式的m,k恒成立.
因为 =
= ,
,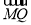 =(4-x1,4k+m),
=(4-x1,4k+m),
由 ·
·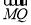 =0,得-
=0,得-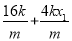 -4x1+
-4x1+ +
+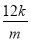 +3=0,
+3=0,
整理,得(4x1-4)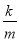 +
+ -4x1+3=0.(**),方程无解.
-4x1+3=0.(**),方程无解.
故不存在定点M,使得以PQ为直径的圆恒过点M.
审题引导:(1)建立方程组求解参数a,b,c;(2)恒成立问题的求解;(3)探索性问题的一般解题思路.
规范解答:【解析】
(1)因为AB+AF2+BF2=8,
即AF1+F1B+AF2+BF2=8,(1分)
又AF1+AF2=BF1+BF2=2a,(2分)
所以4a=8,a=2.又因为e=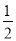 ,即
,即 =
=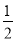 ,所以c=1,(3分)
,所以c=1,(3分)
所以b=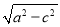 =
=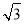 .故椭圆E的方程是
.故椭圆E的方程是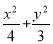 =1.(4分)
=1.(4分)
(2)由 消去y得(4k2+3)x2+8kmx+4m2-12=0.(5分)
消去y得(4k2+3)x2+8kmx+4m2-12=0.(5分)
因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,(6分)
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.(*)(7分)
此时x0=-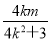 =-
=-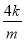 ,y0=kx0+m=
,y0=kx0+m=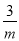 ,所以P
,所以P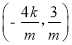 .(8分)
.(8分)
由 得Q(4,4k+m).(9分)
得Q(4,4k+m).(9分)
假设平面内存在定点M满足条件,由图形对称性知,点M必在x轴上.(10分)
设M(x1,0),则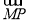 ·
·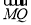 =0对满足(*)式的m,k恒成立.
=0对满足(*)式的m,k恒成立.
因为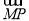 =
= ,
,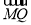 =(4-x1,4k+m),
=(4-x1,4k+m),
由 ·
·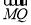 =0,得-
=0,得-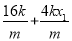 -4x1+
-4x1+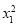 +
+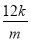 +3=0,
+3=0,
整理,得(4x1-4)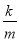 +
+ -4x1+3=0.(**)(12分)
-4x1+3=0.(**)(12分)
由于(**)式对满足(*)式的m,k恒成立,所以 解得x1=1.(13分)
解得x1=1.(13分)
故存在定点M(1,0),使得以PQ为直径的圆恒过点M.(14分)
错因分析:本题易错之处是忽视定义的应用;在处理第(2)问时,不清楚圆的对称性,从而不能判断出点M必在x轴上.同时不会利用恒成立求解.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第5课时练习卷(解析版) 题型:解答题
自点A(-3,3)发出的光线l射到x轴上,被x轴反射,反射光线所在的直线与圆C:x2+y2-4x-4y+7=0相切.求:
(1)光线l和反射光线所在的直线方程;
(2)光线自A到切点所经过的路程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第3课时练习卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,已知点A为椭圆 =1的右顶点,点D(1,0),点P、B在椭圆上,
=1的右顶点,点D(1,0),点P、B在椭圆上, =
= .
.

(1) 求直线BD的方程;
(2) 求直线BD被过P、A、B三点的圆C截得的弦长;
(3) 是否存在分别以PB、PA为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第3课时练习卷(解析版) 题型:填空题
已知直线x+ay=2a+2与直线ax+y=a+1平行,则实数a的值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:解答题
设A1、A2与B分别是椭圆E: =1(a>b>0)的左、右顶点与上顶点,直线A2B与圆C:x2+y2=1相切.
=1(a>b>0)的左、右顶点与上顶点,直线A2B与圆C:x2+y2=1相切.
(1)求证: =1;
=1;
(2)P是椭圆E上异于A1、A2的一点,若直线PA1、PA2的斜率之积为- ,求椭圆E的方程;
,求椭圆E的方程;
(3)直线l与椭圆E交于M、N两点,且 ·
· =0,试判断直线l与圆C的位置关系,并说明理由.
=0,试判断直线l与圆C的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,椭圆C: =1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
=1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.

(1)求椭圆C的标准方程;
(2)若θ=90°, ,求实数m;
,求实数m;
(3)试问 的值是否与θ的大小无关,并证明你的结论.
的值是否与θ的大小无关,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:填空题
以双曲线-3x2+y2=12的焦点为顶点,顶点为焦点的椭圆的方程是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:解答题
已知曲线E:ax2+by2=1(a>0,b>0),经过点M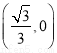 的直线l与曲线E交于点A、B,且
的直线l与曲线E交于点A、B,且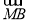 =-2
=-2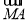 .
.
(1)若点B的坐标为(0,2),求曲线E的方程;
(2)若a=b=1,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练文数学卷(解析版) 题型:选择题
 分别是双曲线
分别是双曲线 的左右焦点,过点
的左右焦点,过点 的直线
的直线 与双曲线的左右两支分别交于
与双曲线的左右两支分别交于 两点。若
两点。若 是等边三角形,则该双曲线的离心率为( )
是等边三角形,则该双曲线的离心率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com