
分析 ①根据二项分布的公式进行求解,
②根据正态分布的对称性结合概率关系进行i区就
③根据积分的几何意义进行求解判断,
④根据期望和方差的公式进行判断.
解答 解:①∵随机变量X服从二项分布B(6,$\frac{1}{2}$),
∴P(X=3)=${C}_{6}^{3}$($\frac{1}{2}$)3×(1-$\frac{1}{2}$)3=$\frac{5}{16}$.故①正确,
②已知随机变量X服从正态分布N(2,σ2) 且P(X<4)=0.9,则P(X>4)=P(X<0)=1-0.9=0.1,
则P(0<X<2)=0.5-0.1=0.4,故②正确,
③根据积分的几何意义得${∫}_{-1}^{0}$$\sqrt{1-{x}^{2}}$dx表示-1≤x≤0,对应$\frac{1}{4}$单元圆的面积$\frac{π}{4}$,${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx表示0≤x≤1,对应$\frac{1}{4}$单元圆的面积$\frac{π}{4}$,
故${∫}_{-1}^{0}$$\sqrt{1-{x}^{2}}$dx=${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx=$\frac{π}{4}$成立,故③正确,
④E(2X+3)=2E(X)+3,D(2X+3)=4D(X),故④错误,
故答案为:①②③
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.


科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 实验班 | 25 | 45 | |
| 非实验班 | 10 | 45 | |
| 总计 | 90 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
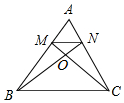 如图,在△ABC中,MN∥BC,$\frac{AM}{MB}$=$\frac{1}{2}$,MC,NB交于点O,若△OMN的面积等于a,得△OBC的面积等于9a.
如图,在△ABC中,MN∥BC,$\frac{AM}{MB}$=$\frac{1}{2}$,MC,NB交于点O,若△OMN的面积等于a,得△OBC的面积等于9a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2016i | B. | 1+2016i | C. | 2016+i | D. | 2016-i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com