
图1-2-15
科目:高中数学 来源:2013-2014学年广东省“十二校”高三第2次联考文科数学试卷(解析版) 题型:解答题
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图3所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
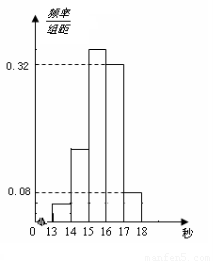
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图1-2(3)-15,某炮兵阵地位于A点,两观察所分别位于C、D两点.已知△ACD为正三角形,且DC=

查看答案和解析>>
科目:高中数学 来源: 题型:

图1-3-15
(1)求证:△ABC∽△FCD;
(2)若S△FCD?=5,BC=10,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com