
【题目】随着移动互联网的发展,越来越多的人习惯用手机应用程序(简称app)获取新闻资讯.为了解用户对某款新闻类app的满意度,随机调查了300名用户,调研结果如表:(单位:人)
青年人 | 中年人 | 老年人 | |
满意 | 60 | 70 | x |
一般 | 55 | 25 | y |
不满意 | 25 | 5 | 10 |
(1)从所有参与调研的人中随机选取1人,估计此人“不满意”的概率;
(2)从参与调研的青年人和中年人中各随机选取1人,估计恰有1人“满意”的概率;
(3)现需从参与调研的老年人中选择6人作进一步访谈,若在“满意”、“一般”、“不满意”的老年人中各取2人,这种抽样是否合理?说明理由.
【答案】(1)![]() (2)
(2)![]() (3)这种抽样不合理,详见解析
(3)这种抽样不合理,详见解析
【解析】
(1)根据古典概型的概率公式进行计算即可
(2)根据独立事件同时发生的概率公式进行计算即可
(3)根据抽样的公平性的性质进行判断
(1)从所有参与调研的人共有300人,不满意的人数是25+5+10=40,
记事件D为“从所有参与调研的人中随机选取1人此人不满意”,
则所求概率为![]() .
.
(2)记事件M为“从参与调研的青年人中随机选取1人,此人满意”,则![]() ;
;
记事件N为“从参与调研的中年人中随机选取1人,此人满意”,则![]() ;
;
则“从参与调研的青年人和中年人各随机选取1人,恰有1人满意”的概率为![]() .
.
(3)这种抽样不合理.
理由:参与调研的60名老年人中不满意的人数为20,满意与一般的总人数为x+y=50,说明满意度之间存在较大差异,所以从三种态度的老年中各取2人不合理.合理的抽样方法是采用分层抽样,根据x,y,10的具体数值来确定抽样数值.


科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,
中,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,点
的中点,点![]() 在对角线
在对角线![]() 上运动.当
上运动.当![]() 的面积取得最小值时,点
的面积取得最小值时,点![]() 的位置是( )
的位置是( )

A.线段![]() 的三等分点,且靠近点
的三等分点,且靠近点![]() B.线段
B.线段![]() 的中点
的中点
C.线段![]() 的三等分点,且靠近点
的三等分点,且靠近点![]() D.线段
D.线段![]() 的四等分点,且靠近点
的四等分点,且靠近点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某广告商租用了一块如图所示的半圆形封闭区域用于产品展示,该封闭区域由以![]() 为圆心的半圆及直径
为圆心的半圆及直径![]() 围成.在此区域内原有一个以
围成.在此区域内原有一个以![]() 为直径、
为直径、![]() 为圆心的半圆形展示区,该广告商欲在此基础上,将其改建成一个凸四边形的展示区
为圆心的半圆形展示区,该广告商欲在此基础上,将其改建成一个凸四边形的展示区![]() ,其中
,其中![]() 、
、![]() 分别在半圆
分别在半圆![]() 与半圆
与半圆![]() 的圆弧上,且
的圆弧上,且![]() 与半圆
与半圆![]() 相切于点
相切于点![]() .已知
.已知![]() 长为40米,设
长为40米,设![]() 为
为![]() .(上述图形均视作在同一平面内)
.(上述图形均视作在同一平面内)
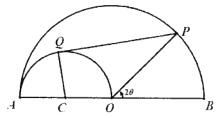
(1)记四边形![]() 的周长为
的周长为![]() ,求
,求![]() 的表达式;
的表达式;
(2)要使改建成的展示区![]() 的面积最大,求
的面积最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为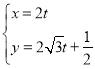 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设动点![]() 在圆
在圆![]() 上,动线段
上,动线段![]() 的中点
的中点![]() 的轨迹为
的轨迹为![]() ,
,![]() 与直线
与直线![]() 交点为
交点为![]() ,且直角坐标系中,
,且直角坐标系中,![]() 点的横坐标大于
点的横坐标大于![]() 点的横坐标,求点
点的横坐标,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com