
有一个不透明的袋子,装有4个完全相同的小球,球上分别编有数字1,2,3,4.
(Ⅰ)若逐个不放回取球两次,求第一次取到球的编号为偶数且两个球的编号之和能被3整除的概率;
(Ⅱ)若先从袋中随机取一个球,该球的编号为a,将球放回袋中,然后再从袋中随机取一个球,该球的编号为b,求直线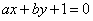 与圆
与圆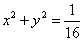 有公共点的概率.
有公共点的概率.
解:(I)用(a,b)(a表示第一次取到球的编号,b表示第二次取到球的编号)表示先后二次取球构成的基本事件,则基本事件有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12个.
设“第一次取到球的编号为偶数且两个球的编号之和能被3整除”为事件A,
则事件A包含的基本事件有:(2,1),(2,4),(4,2)共有3个,
∴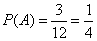
(II)基本事件有(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共16个,
设“直线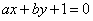 与圆
与圆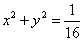 有公共的”为事件B,由题意
有公共的”为事件B,由题意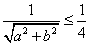 ,
,
即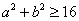 ,则事件B包含的基本事件有(1,4),(2,4),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共8个,
,则事件B包含的基本事件有(1,4),(2,4),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共8个,
∴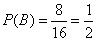 .
.


科目:高中数学 来源: 题型:
已知球O的半径为4,圆M与圆N为该球的两个小圆,AB为圆M与圆N的公共弦,AB=4
若OM= ON.则两圆圆心的距离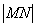 的最大值为
的最大值为
(A)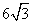 (B)
(B) 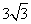 (C)
(C) 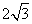 (D)3
(D)3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com